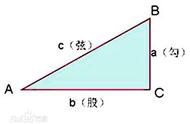
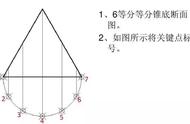
同学们好,我是刘小龙老师。今天来看一个关于正六边形的题,题目就不读了。o是圆心,m与n都是中点。
·第一个扇形omn,把扇形变成一个圆锥,圆锥的底面半径是r1,所以需要将弧mn的弧长表示出来,因为1/2πr1就等于弧mn的弧长。
·efd扇形变成一个圆锥,它的半径是r2,相当于需要将df的弧长求出来,就等于1/2πr2。
·再来看一下这个题,不要计算,用等比例算法,圆锥的展开图形实际上就是扇形弧长变成了圆锥的底面的圆。

·还有个是六边形的边心距。首先看一下六边形,正六边形的每一个角的度数都是一样,可以变成两个、三个、四个三角形,四个三角形每一个三角形是180度,内角和一共是有6个角,所以每一个角的度数都是120度,也就是角e的度数是120度,由多边形的内角和可以得到角的度数。

·再来看这个角,这个角将它连接一下,oab就是一个等边三角形,所以这个角是60度,m、n都是中点,两边都是30度,所以角m、o、n度数也是120度,弧mn的长度就可以表示成360分之120,再乘以2πom,om就是半径。
相同的道理,下面扇形也是360分之120度,这个角是120度,所以是120度,再乘以2π,它的半径是ef。

观察一下这两个式子,需要求r1比r2,所以,将上面的式子与下面的式子左边比左边等于右边比右边,直接就得到了答案。所以r1比上r2实际上就变成了OM的长度比上EF的长度,就是OM的长度是与EF的长度,就是求的一个边心距。
将它放到三角形OAF中,这个三角形是一个等边三角形,所以如果假设EF的长度是n,那么AF就是a,那么AM的长度就是二分之n。根据30度的直角三角形三边关系,一二二跟上三,所以AM是二分之n,那么OM的长度就是二分之n再乘以根号三,二分之根号三n,而EF的长度就是边长n,就直接得到了答案,二分之根号三还是比较简单的。

有一些题不需要将它所有的长度结果算出来,只需要用等比例算法简化计算就可以了。也就是说运用一式与二式上下相除就直接能够得到答案。希望这种方法能够减少同学们的运算。本期视频就到这里,谢谢观看。
,