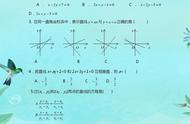
学习解析几何时要随时注意联系平面几何的知识。要经常利用平面几何中的定理来简化问题中的条件与推理过程(在例1中,我们就是这样做了)还要利用平面几何的性质作为对解答的一种直观检验。本例得出了三条直线,可能已经很出一些同学的意外。但如果用平面几何的方法一思考,那就很容易知道应该有四条直线(见图)。那么,还有一条到哪里去了?一研究,发现


除了x=3),只是凑巧x=3不是所求的解,因而没有引出错误罢了。
这个例子告诉我们,应该注意各类直线方程不包括哪些直线。点斜式(斜截式)不包括与 y 轴平行的直线,截距式不包括与x、y 轴平行的直线、法线式和一般式则没有上述限制。因此,例2如用后两种直线方程做,都可以求出四条直线,只是运算复杂些。同学们不妨试试。
最后,列出几个题目供同学们练习。
1、已知等腰直角三角形斜边所在的直线方程为 3x-y 5=0,直角顶点为(4,1),求两条直角边所在直线的方程。
2、设直线2x y=1为三角形一内角平分线,点(1,2)与(-1,-2)为三角形两顶点,求其第三顶点。
3、已知直线过点(-1,-4),它在两坐标轴上的截距为负值,且其积为最小,求此直线方程。
4、已知直线过点(-1,1),且与两坐标轴围成三角形的面积等于3,求其方程。
5、一直线过点(-1,1),它被两平行直线
x 2y=1与x 2y=3
所截得线段的中点在直线x-y=1上,求其方程。
6.已知直线被两平行直线
3x 4y 8=0与3x 7y-7=0
所截得线段长为3√2,并过点(2,3),求其方程。
7,设 f(x,y)=a₀x³ a₁x²y a₂xy² a₃y³=0表示三条直线,则点 P ( m,n)到此三直线的距离之积为