(若四边形ABCD内接于⊙O,则AC•BD=AD•BC AB•DC)

若四边形ABCD为圆内接四边形,则对角线AC与BD的乘积等于一对对边AB与CD的乘积加上另一对对边AD与BC的乘积,即AC·BD=AB·CD AD·BC。
证明:
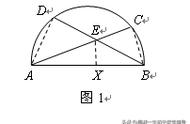
如下图所示:

设∠ACB大于∠ACD,则在∠ACB内作一个以点C为顶点、以CB为一边的∠BCE,使∠BCE=∠ACD(图中的红色角)。
∵∠CAD=∠CBE(同弧同侧的圆周角相等),
∴三角形ACD∽BCE,
∴AD : BE = AC : BC,即AD·BC=AC·BE①
同理,三角形CDE∽ABC,
∴CD :AC = DE :AB,即AB·CD=AC·DE②
① ②=AD·BC AB·CD=AC·(BE DE)=AC·BD
即:AC•BD=AB•CD AD•BC
三、典型例题
(1)