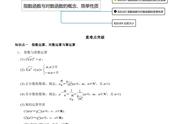
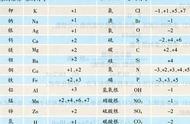
一、引言
对数作为数学中的重要概念,在解决复杂数学问题和实际应用中发挥着关键作用。它不仅是数学分析的基础,还在物理、化学、工程、经济等领域有着广泛的应用。本文将对“对数的概念”这一知识点进行详细解析,帮助同学们更好地掌握这一内容。

二、对数的定义
- 对数的定义:如果a^x = N(a > 0且a ≠ 1),那么x叫做以a为底N的对数,记作x = logaN。其中,a叫做对数的底数,N叫做真数。
- 常用对数:以10为底的对数叫做常用对数,记作lgN。例如,lg100 = 2,表示10的2次方等于100。
- 自然对数:以自然数e(约等于2.71828)为底的对数叫做自然对数,记作lnN。例如,ln(e^2) = 2,表示e的2次方等于e^2。
三、对数的性质
- 对数的运算法则:
- 乘法法则:loga(MN) = logaM logaN。表示以a为底的两个数的乘积的对数等于这两个数对数的和。
- 除法法则:loga(M/N) = logaM - logaN。表示以a为底的两个数的商的对数等于被除数的对数减去除数的对数。
- 指数法则:loga(M^n) = n * logaM。表示以a为底的一个数的n次方的对数等于这个数的对数与n的乘积。
- 换底公式:logbN = (logaN) / (logab)。表示以b为底N的对数可以转化为以a为底的对数进行计算。这个公式在解决复杂对数问题时非常有用。
- 对数的性质:
- 任意数的0次方都为1,所以logaa=1。
- 真数为1时,任何底数的对数值都为0,即loga1=0。
- 对数函数在其定义域内是单调的,当底数大于1时,函数单调递增;当底数在(0,1)之间时,函数单调递减。
四、对数函数及其图像
- 对数函数的定义:形如y = logax (a > 0且a ≠ 1) 的函数称为对数函数。其中x是自变量,函数的定义域是(0, ∞)。
- 对数函数的图像:对数函数的图像是一条曲线,当a > 1时,图像上升;当0 < a < 1时,图像下降。这条曲线在x轴上方,y轴右侧,且随着x的增大而无限趋近于x轴。
- 对数函数的性质:对数函数在其定义域内是连续的,且在其定义域内具有单调性。此外,对数函数还具有一些特殊的性质,如过定点(1,0)等。
五、应用举例
- 计算复杂运算:利用对数的运算法则和换底公式,可以将复杂的乘除运算转化为简单的加减运算,大大简化计算过程。例如,在计算大数的幂或开方时,使用对数可以显著减少计算量。
- 解决方程和不等式:通过对数方程的转换,可以解决一些复杂的代数方程和不等式问题。例如,通过取对数可以将指数方程转化为线性方程进行求解。
- 在物理和化学中的应用:在物理和化学中,很多自然现象可以用对数函数来描述。例如,声音的强度与距离的关系、放射性元素的衰变等都可以用对数来表示和分析。
- 在工程和经济中的应用:在工程和经济领域中,很多实际问题可以通过建立对数模型来解决。例如,在工程中计算材料的疲劳寿命、在经济中分析复利增长等都可以利用对数进行建模和分析。
六、总结与展望
通过本文的学习,同学们对“对数的概念”这一知识点有了更深入的理解。掌握这一知识点不仅有助于提高学生的数学素养和解决问题的能力,还为后续的学习和应用奠定了坚实的基础。希望同学们在未来的学习中不断巩固和应用这一知识点,探索更多与之相关的有趣性质和应用实例。同时,也期待教育工作者和研究者们能够不断完善和拓展这一领域的教学内容和方法,为学生提供更加优质的教育资源和指导。通过不断地学习和实践,我们相信同学们一定能够熟练掌握这一知识点,并在实际生活中加以应用。
,