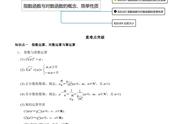
若函数,则值域指的是或的取值范围,就是你有没有什么方法能找到函数的最大值和最小值.这个对于基础函数而言,是比较容易看得出来,但复杂的函数就不是这么容易,下面我将从十六个方面给大家介绍如何求函数的值域,在这里还是说一下,创作不易,若我的文章对你有帮助,麻烦大家帮忙点个关注,谢谢!
观察法
观察法通常只能解决一些基本初等函数,例如初中学的一次函数、反比例函数;高中学的基本初等函数:幂函数、指数函数、对数函数和三角函数.
下面直接把以上说到的函数一一列举出来加以说明:
1、若函数是一次函数(或正比例函数)则值域因为一次函数图像是直线,没有大小可言的,故不可能有最大值,也没有最小值;
2、若是反比例函数(含左右平移模型)则值域是
3、若函数则值域是
4、若则值域是
5、若是幂函数这种情况就要特殊点,下面举几个例子说明一下:
①当的值域是
②当的值域是
③当函数的值域是
④当函数的值域是
⑤当函数的值域是
注意:以上五种情况只是部分,并不能代表所有种可能,同学们要注意区分.
6、若是三角函数:
①正弦函数的值域是
②余弦函数的值域是
③正切函数 的值域是
分离常数法
分离常数法主要是钟对分式型函数模型:
这种方法各位同学要注意在分离时不能再引入,不然你的分离是失败的,同时也不建议去记分离的公式.具体做法为:
①分母有什么分子就写什么;
②再进行恒等配凑,只能引进常数的相关运算,不能再引入新的进行配凑.
下面举例加以说明:
例1:求函数的值域.
分析:
而:
例2:求函数的值域.
分析:
反函数法
高中学过的函数基本上都存在反函数,下面先介绍一下反函数:
设函数的定义域为值域为如果对每一个必存在唯一的使得成立,则由此定义了一个新的函数这个函数就称为函数的反函数,一般记作它的定义域为值域为相对于反函数而言,原来的函数称为直接函数.但同学们可能要注意以下两点:
①严格单调函数必有反函数;
②与本质上是同一个函数,只是前者是用表示后者是用表示(这就是我们用反函数求函数值域的原因,值域不好求,转化成求它反函数的定义域,求定义域总比求值域容易)
③原函数(直接函数)与它的反函数的图像头于直线对称.
通过上面的讲解,我们可以拿上面的分式型函数模型:
试一下.
还是上面的例子说明一下:
例1:求函数的值域.
分析:
例2:求函数的值域.
分析:
配方法
当所给函数是二次函数或可化为二次函数模型:
可利用配方法求函数的值域.
注意:这种方法不能笨拙的去使用,而要用得比较快,就要脱离初中思维,具体可以这样思考:
①求二次函数的对称轴:
②根据二次函数二次项系数的正负,画出函数草图,不要求精准,只要求大概;
③标具体题目研究的区间;
④直接求出最大值和最小值,此时就得到值域.(因为高中考题基本不会像初中一样多数题目都考虑可以取任意数)
下面举例说明一下:
例1:若,求函数的值域.
分析:
例2:求函数的值域.
分析:
判别式法
此方法是针对于分式型函数:
其原理是本身给定的函数一旦给定一个那么必有唯一的与之对应,故把原函数转化成一元二次方程模型,则以为变量的方程必有实数根.同时要注意以下两点:
①有时要注意分类讨论;
②一定要把当成常数处理.
下面举例加以说明:
例:求函数的值域.
分析:
换元法
这种方法主要针对的是含有二次根式或复合函数:
的模型,方法就是把最复杂(或最关键)的部分令为,这里一定要注意的取值范围,再把原函数中所有与有关的部分都换成含有的式子,最终变成再求函数的值域,最终就得到目标函数的值域.
下面举例说明:
例1:求函数的值域.
分析:
接下来采用配方法求出:
例2:求函数的值域.
分析:
根据分离常数法得:
函数单调性法
若知道一个函数在研究的定义域上的单调性,则可以用此方法.这种方面在高中更多的是分两种情况:
①若对于任意的都有则函数在上单调递增,此时在区间端点处取到最值;
②若对于任意的都有则函数在上单调递减,此时在区间端点处取到最值.
下面举例说明:
例1:求函数的值域.
分析:
例2:求函数的值域.
分析:同理可得
不等式法
在高中更多的是利用常用不等式或者均值不等:
下面举例说明:
例:求函数的值域.
分析:
函数有界性法
设的定义域为有如果存在某个正数使对任意的使对任意的有则称在上有界.高中而言,不能理解概念也没有什么大不了.
下面用最简单的例题讲解感觉抽象的东西:
例:求函数的值域.
分析:
数形结合法
这类方法主要的是针对含有绝对值的函数,其题型是函数解析式具有明显的某种几何意义,如两点的距离公式直线斜率等等,这类题目若运用数形结合法,往往会更加简单,一目了然,赏心悦目.
以下举例说明一下:
例:求函数的值域.
分析:
如下图:

一一映射法
这种方法更多的是用到分式型函数:
上,其原理是在定义域上与是一一对应的.故两个变量中,若知道一个变量范围,就可以求另一个变量范围.
例:求函数的值域.
分析:
图象法
对于给定图像或函数及容易画出草图的,我们直接可以从图像上得到函数值域的范围.这种方面在实际问题中分段函数常用此方法.
利用多项式的除法

这种主要是针对于分式型函数模型:
本质上大同小异,这里就不再展开讲解.

构造法
根据函数的结构特征,赋予几何图形,数形结合.如下面这个例子: