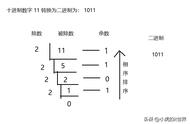
作者,Geek学院,哆嗒数学网群友
关注 哆嗒数学网 每天获得更多数学趣文
相信大家对双扭线的形状都不会感到陌生,今天我们就来聊聊它的方方面面。
一、作为数学对象的双纽线
双纽线 或者说lemniscate ,词源是拉丁语“lemniscus ”,古希腊语λημνῐ́σκος(lēmnískos),即指缎带。确切地说,双纽线在数学中指代着多种不同缎带般的8字形曲线,但一般特指伯努利双纽线 (Lemniscate of Bernoulli )。它不仅是所有双纽线中最为人们熟知的,同时数学上也是内涵最丰富的几何对象之一。
直角坐标系下,半径为a的伯努利双纽线是由下述四次多项式方程
(x² y²)²=a²(x²-y²)
给出的隐函数的图像,例如

就是半径为1的双纽线,这里的半径指的是中心到最远端点的距离。
由定义可知双纽线是某个(二元)四次多项式在平面上的零点,所以双纽线是一条四次平面曲线(quartic plane curve ),从而也是一条代数曲线。对定义稍加分析不难发现,就像圆一样,不同半径的双纽线都是彼此相似的,换句话说双纽线的形状是唯一的。应用一元二次方程的知识,容易通过计算发现半径为1的双纽线高为√2/4。
二、伯努利双纽线的诞生
双纽线的英文单词“lemniscate”最早于1694年被雅各布·伯努利 (Jacob Bernoulli ,1654-1705)用来描述他所发现的双纽线,他为了解决莱布尼兹的等时曲线问题,想找到一条和某(工程力学相关的)超越曲线有相同弧长函数的代数曲线提出了这条曲线。1694年9月《教师学报》(Acta Eruditorum )发表了雅各布的这项研究。下图是1695年12月雅各布发表的研究中的配图,描绘了伯努利双纽线与等时曲线的关系:

巧合的是,雅各布·伯努利的弟弟约翰·伯努利 (Johann Bernoulli ,1667-1748)为了解决莱布尼兹的等时曲线问题也独立发现了伯努利双纽线,然而1694年10月《教师学报》(同一份期刊)上才发表了他的结果,仅仅晚了一个月。毫无疑问,争执解答等时问题的优先权成了兄弟间的无数纷争之一。
值得一提的是,早在1680年著名天文学家卡西尼 (Cassini ,1625-1712)提出过一族曲线即卡西尼卵形线 (Cassini oval )试图来描述地球与太阳相对运动轨迹(虽然卡西尼对土星研究有着巨大贡献,但这一点他完全是迷信了)。伯努利双纽线便是卡西尼卵形线的特例,但毕竟出发动机不同,卡西尼从未注意过它,所以数学史上将伯努利双纽线的发现归功于伯努利们是完全合适的。
有一些资料指出,伯努利双纽线的诞生是对椭圆定义的简单推广,也就是到两定点之积为定值的曲线。虽然这个定义正确并且自然,但这是完全不符合史实的。这种曲线就是卡西尼卵形线,然而不论是伯努利双纽线还是卡西尼卵形线,上述史料告诉我们历史上都有着更强有力的动机让人们提出它。现实数学中,几乎每个重要概念提出的动机都是只有考察数学史才可能得知的强有力的动机,数学中几乎没有任何一个重要概念的提出动机仅仅是由于形式上简单自然的,因为这不足以让人有必要去发展它。
三、作为符号的双纽线
毫无疑问,每个人看到伯努利双纽线以后都会想到无穷大,很让人怀疑是不是规定过无穷大的记号就得长成伯努利双纽线的样子,然而并没有过这种规定。
1655年,数学家沃利斯 (Wallis ,1616-1703)在其著作中用符号“∞ ”作为无穷大的记号 :

失望的是,他完全没有说明任何理由。有一种推测是它长得像罗马数字里的1000,即“CIƆ”,因为有时会用它表示“许多”的概念,还有一种推测是认为和最后一个希腊字母“ω”长得像。
虽然据其形状可以称之为双纽线,但此时和伯努利双纽线绝对没有任何关系,因为这是它被发现前39年的事情,此后两者之间也依旧没有直接关联。简而言之,表示无穷大用的双纽线就只是一条长得好看点的双纽线而已。双纽线作为符号,在社会文化中也逐渐频繁出现,现在几乎是无处不在了。它不仅用来表示无穷大,也逐渐承载了越来越多的含义,这些含义往往与各种神秘概念相关。
可以相信的是,在Wallis之前,双纽线并不会作为符号承担任何含义。所有以双纽线作为符号的事情,必定是Wallis之后的了。
关注 哆嗒数学网 每天获得更多数学趣文
,