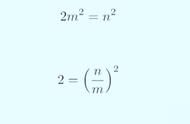矩阵的阶数是对矩阵中的方阵而言的,它指的是方阵的行数(或列数)。

下面详细地来介绍下矩阵和方阵的概念。
矩阵概念。矩阵本质上就是一些元素构成的表,它是大学数学中高数和高等代数中的内容。高数和高等代数里研究的矩阵的元素是数,对应的矩阵就是一个数表。
矩阵分类。一、按矩阵形状(行数和列数)分类
1.一般矩阵。
一个矩阵m行,n列的矩阵又称为矩阵。其中,m和n都是大于或等于1的自然数。一般情况下,m和n可以相等也可以不相等。
2.方阵。
如果一个矩阵的行数和列数相等,那么这类矩阵又称为方阵。方阵中,一个m行m列的方阵又叫做m阶矩阵,我们称它的阶数为m。一个n行n列的方阵又叫做n阶矩阵,我们称它的阶数为n。

二、按矩阵的元素来分类。
1.如果一个矩阵中的元素全都是0,我们就称其为零矩阵。
【注意】只有行数列数都相等,并且对应位置的元素完全相同的矩阵才是相等矩阵。所以,任意两个零矩阵间不一定相等。因为行数和列数不一定相同。
2.如果一个矩阵的主对角线(或次对角线)以外的元素全为0,则称为对角阵。
3.如果一个n阶方阵的主角线上的元素都是1,主对角线以外的元素都是0,则称这样的矩阵为n阶单位矩阵。
【注】和零矩阵不一定相等外,单位矩阵也不一定相等(因为单位矩阵间的阶数不一定相同)。

1.矩阵的阶数是针对方阵而言的。
2.方阵是行数和列数都相等的矩阵。
3.方阵的行数(或列数)又称为方阵的阶数。
4.不是方阵的矩阵要同时点名矩阵的行数和列数,如一个m行n列的矩阵常称为矩阵。
5.所有的单位矩阵必然都是方阵。
,