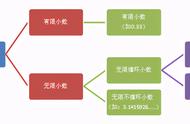
循环小数化成分数的规律。
上一节主要学习了全循环小数化成分数,它的规律就是根据循环结来确定分母。一个循环结就分母写作9,两个循环结写成9之1,三个循环结写成9之9。用循环结来确定9的个数,分子就是它的循环结。
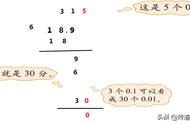
这一节来学习的是混循环小数如何化成分数。混循环小数化成分数要与纯循环小数化成分数的方法结合起来,也可以设a等于零点八三的循环。
·首先找到循环节的位置,循环节的位置前面有一个八,这时候需要把八画到循环节前面化为整数部分,就变成十a。如果乘以十一号,它的部分是八循环结还是三的循环?根据循环结的规律还需要再乘以一百,零点八三的循环乘以一百就等于八三点三的循环。

·这时候用一百a减去十a,为什么要用一百a减去十a?目标是消去后面的循环角数,一百a减去十a就等于八十三点三的循环减去八减三的循环。循环小数还是三的循环,用整数部分减去整数部分,小数部分减去小数部分,一百a减去十a就等于九十a。

·小数部分减小数分等于零,整数部分用八十三减去八等于七十五,那么a就等于九十分之七十五。然后进行约分就等于六分之五。

总结一下混循环角数化成分数的规律。看到这只是有一个循环节,而它的分母划目的只有一个九,而后面多了一个零。为什么会多了一个零?因为它有一位不是循环节的部分。可以总结规律,循环节确定分母9的个数,循环节的前面有分循环的小的部分就在9的后面补零,有一位补一个零,有两位补两个零。