请不要忽视这个定理,它非常具有魅力,解决它的过程,得出的推论也非常具有魅力,而这个定理及推论可能是非常重要的认知自然的线索。
一、传承2000多年未被证明的定理
有一个定理,听起来很简单,但证明起来很麻烦。它就是周长定理,该定理的完整表述如下:周长相等的平面封闭图形中圆形的面积最大。
这个定理看起来很简单,简单举例验证其结果也完全正确。于是,人们就一定把这个结论看作理所当然的,当成公理一样来使用。这个问题从首次被芝诺多罗斯(公元前200年到公元前140年)正式提出,但并没有给出详细证明,只是指出了几个步骤:1、周长相等的多边形中,正多边形面积最大;2、周长相等的多边形中,边的数量越多面积越大;3、周长相等的图形中,圆形的面积最大。这个看起来就像是基于直觉和几何作图后的猜想。
后来,古希腊数学家帕普斯(大约公元290年到公元350年)在他的《数学汇编》中收纳了这一结论,并做出了发展,周长相等的弓形图形中,半圆的面积最大。同样,他也没给出证明过程。(但是,弓形面积最大定理必须是周长不包含底边才是成立的,否则它是错误的!比如半径为1时,半圆的面积为0.5π<1.58,周长为π 2;此时周长为π 2的正方形面积为 [(π 2)/4]^²>1.64,很明显正方形面积更大,也就是说,不能用周长这个词来表达,其易错的症结后续分析)
二、周长定理的首次证明
后来,这个问题的证明一直被数学界回避着。哪怕一些声名煊赫的大数学家,他们也是理所当然地使用这个结论,就是不给详细证明过程。
直到1839年,德国出了一位非常了得的几何天才,叫做雅克布,他很天才地提出了三部曲证明周长定理:1、面积最大的多边形,其任意两条邻边围成的角必然是凸角。(因为如果是围成的角是凹角,利用镜像原理和反证法很容易证明必然存在一个与它周长相等的凸角多边形比它的面积大;)2、当面积最大时,在凸角多边形的周边上取两点使得周长被等分,则该两点连线也必然等分该多边形的面积。(这个同样还是用反证法证明,因为如果面积不等分,而周长等分,那么将面积较大的部分以该两个点连线镜像,得到一个面积更大的图形,这与面积最大的假定矛盾);3、当面积最大时,其半周长所围成的弓形图形必然为半圆。(因为半周长的两个端点A、B所连线段在半圆周上任一点C连线中,只有当AC⊥BC时,才符合最大的面积的前提)
按说,雅克布的证明非常天才,也非常好理解。但是这里面有一个逻辑前提,就是雅克布假定存在面积最大的图形,并且反复使用了这个论点作支撑,证明了圆周定理的结论。也就是说,圆周定理中有两个结论:1、周长一定的封闭平面图形中,存在着一个最大面积的图形;2、这个面积最大的图形是圆形。
可能有人会说,很简单啊,有限周长围成的封闭平面图形,很明显就是存在一个面积上限的。但是对不起,数学逻辑不承认直觉,而是要严格推导,否则也不用证明周长定理了。
这样,再过了几十年,1870年时,另一位德国科学家,利用变分法的方式严格证明了这个定理。
三、其他证明方式的探索
为了探求这个问题,我们尝试用一般性的知识来求证一下这个定理。为了表明这个过程用到知识的一般性,我们尽量不画图,只用公式和文字来表述。(哈哈,其实主要是不知道怎么画上去,还好,叙述起来也不麻烦)
我们相信,越是原始的笨功夫,挖掘的规律可能也越多,越普遍,我们结合天才雅克布的部分思路,同时按照芝诺多罗斯的思考方式证明一下。
1、 周长相等的封闭平面多边形中正多边形面积最大
1.1周长相等时,封闭平面多边形中,凸多边形一定比凹多边形面积大
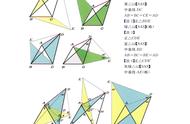
这个很容易用几何方法证明,只需要镜像做图即可。稍微描述一下,比如凹多边形的考察任意一个凹角,必由三个相邻的点A、B、C构成两条相邻的边AB、BC组成,∠ABC为向内凹陷的角,此时把AB、BC沿着AC连线作镜像,得到AB’和BC’而∠AB’C为向外凸出的角,很显然,AB’=AB和BC’=BC,此时得到的新的凸多边形显然大于原来的凹多边形的面积。
1.2三角形面积定理
(1)周长相等的封闭平面三角形中,正三角形面积最大
这有多种办法可以证明,最简单的法子就是利用海伦公式结合三元不等式:
设三角形三条边长为a、b、c,周长的一半P=(a b c)/2,则有面积S=[P(P-a)*(P-b)*(P-c)]1/2。很显然,(P-a)*(P-b)*(P-c)都是>0的正数,也就是三角形任一条边长必小于其他两条边长之和或周长的一半,故有(P-a)*(P-b)*(P-c)≤1/27*[(P-a) (P-b) (P-c)] ^3;所以当(P-a)=(P-b)=(P-c)时,即为等边三角形时,S达到最大值。
等边三角形一定是正三角形。
(2)周长相等且已知一条边长时,封闭平面三角形中,等腰三角形的面积最大
此时,一条边长已知,不妨设为c,另两条边长设为a、b,周长的一半P=(a b c)/2也为已知数,由海伦公式,此时三角形面积为S=[P(P-a)*(P-b)*(P-c)] ^1/2;注意,这里P、P-c都是已知数,只要(P-a)*(P-b)达到最大值,S就是最大值,同样利用二元不等式还是很简单就可以证明只有(P-a)=(P-b)时,面积达到最大。这里用最基本的数学关系推证一下,因为b=2P-c-a,所以(P-a)*(P-b)=(P-a)*[(c-P) a]=-a^2 (2P-c)a P(c-P)={[(2P-c)/2] ^2 P*(c-P)}-[a-(2P-c)/2] ^2,你用初中一元二次方程的知识也可以解出来最大值,但是我们既然知道微积分和极值定理,那就更简单了,另f(a)=-a^2 (2P-c)a P(c-P),∂f/∂a=-2a (2P-c)=0时存在极大值,(为啥不是极小值呢,从上面的式子中可判断出来),此时a=P-c/2,b=2P-c-a= 2P-c -P c/2= P-c/2=a;得证。
1.3周长相等的封闭平面四边形中,正方形的面积最大
我们一直在欧式平面几何中思考,平滑的平面三角形中,不存在凹三角形,所以在1.2的两个结论中,我们不需要讨论凹三角形的情况。
但是,四边形那就必须先排除掉凹四边形的干扰,由1.1的结论知道,凹四边形面积小于凸四边形。要找最大的面积,我们只需要讨论后者。
对于凸四边形ABCD四个点依次相邻,此时我们任取相邻的三个点,不妨为A、B、C,连接AC,由1.2中的第(2)部分结论可知,S△ABC的面积对于任意情形下只有当AB=AC时达到最大,同理可证,只有当凸四边形ABCD的四条边都相等时,面积才可能达到最大值,其余任何情况必有一个面积更大的四边形存在。也就是等周封闭的四边形中,等边的四边形面积大于不等边的四边形。
此时,我们仅需要讨论四条边均相等的凸四边形。它可不像三角形那么简单,还需要证明四个角相等,才能证明这是一个正四边形。
此时,四条边相等的四边形肯定是个平行四边形了,这个结论如果你还实在要证明,随便一连对角线,立刻能证明。平行四边形任周边上的一点向对边做垂线段,不妨取A点向DC做垂线段垂足为E,很显然底边DC的高也就是AE的长度≤另一组对边AD或BC的长度。不等式仅当DC⊥AD时成立,也就是说等周的平行四边形中,只有直角四边形的面积是最大的。四个角都是直角,且边长都相等,此时很明显这个四边形是个正四边形。
而有上述的推证过程可知,我们是一步步压缩四边形的讨论范围的,到了正四边形时候,我们得知其面积最大。我们尽量小心翼翼地避免假设存在一个最大面积的情形,而正向推演,到最后证明等周情况下,正四边形面积大于一切其他四边形。也就是等周四边形中,正四边形的面积最大。
其实,雅克布的求证过程,我觉得有点被存在性给委屈了,换个说法,等周的情况下,圆的面积一定大于其他多边形的面积或许会就避开了反证法的带来的必须证明假设条件存在性的前提了吧。
1.4周长相等时的封闭平面多边形中(边数≥5时),正多边形的面积最大
同样地,首先根据1.1排除凹多边形。
其次,根据1.3同理,任取凸多边形上相邻的三点A、B、C,可知S△ABC的面积对于任意情形下只有当AB=AC时达到最大,也就是说凸多边形任意两条边必须相等,即等周封闭的多边形中,等边的凸多边形面积大于不等边的凸多边形。
在等边的凸多边形中,任取依次相邻的4个点,记作A、B、C、D,可知AB=BC=CD,连接AD,可得四边形ABCD。取BC和AD中点,依次记作E、F,连线得EF。此时,此时你其实需要一个先画个图,否则你接下来估计有点分析障碍,哈哈。
此时,S四边形ABCD= S四边形ABEF S四边形ECDF,对后两者必然有某一个四边形的面积更大或二者相等的情况存在,不妨设ECDF的面积更大,在该四边形中连接ED进行分析可知:S四边形ECDF=S△ECD S△EDF,而在不影响S△ECD的前提下,当DF⊥EF时,S△EDF 大于 CF不垂直于EF情况下的面积,很显然DF⊥EF时的S四边形ECDF 也大于CF不垂直于EF情况下的面积。同理,EB⊥EF时候,S四边形ECDF 也更大。这时有BC∥AD,且中线EF⊥BC和AD。四边形ABCD就是一个等腰梯形,且很特殊,上底还与腰长相等。很容易知道相邻的∠ABC=∠BCD。而如果∠ABC≠∠BCD,则中线EF必然不垂直于BC和AD(利用反证法和全等三角形很容易证明)。也就是说,当AB=CD时,∠ABC=∠BCD是中线EF⊥BC的充要条件。
同理可知,任意相邻的两个角都相等的情况下,即所有的顶角都相等的情况,即正多边形的情况,其面积大于非正多边形的面积。
2、 周长相等时,正多边形边的数量越多,面积越大
接下来,证明边的数量越多,正多边形的面积越大,这个太容易了。正多边形的边数量为N,周长为2P,沿着多边形的中心向所有的边的两个端点连线,则将正多边形分成N个等腰三角形,每个等腰三角形的底所对的顶角为2π/N(这个角的顶点为多边形的中心),此时正多边形的面积为为S=N(小三角形数量)*1/2*2P/N(小三角形的底)*P/[(N*tan(π/N)](三角函数正切值已知底和角,求得高)。
此时,面积S为N的函数,可整理表达为S=N*1/2*2P/N*P/[N*tan(π/N)]=P^2/[N*tan(π/N)]。
令f(N)= N*tan(π/N),对N求导,得知∂f/∂N=tan(π/N)-π/[N*cos^2(π/N)]=[N*sin(π/N)*cos(π/N)-π]/ [N*cos^2(π/N)];而需要注意到N此时≥5,且为整数,π/5≥π/N>0,注意到sin(π/N)<π/N,cos(π/N)<1。则N*sin(π/N)*cos(π/N)-π<N*π/N*1-π=0,也就是说,f(N)是一个减函数,随着N的增大,f(N)递减。
那么S= P^2/[N*tan(π/N)]= P^2/ f(N)就是一个增函数,随着N的增大,S的值增大。
于是得证。
PS:对于sin(π/N)<π/N这个结论,想要证明很简单,画一个半径为1的圆,此时这个圆可以叫做标准圆,它的任意角度对应的弧度在数量上相等,这样角度和长度就可以进行数量值上的比对了。角度为π/N时,sin(π/N)的长度必然小于角度为π/N所对应的弧长π/N。
3、 周长相等时,所有的图形中,圆的面积最大
如何证明圆形的面积大于一切正多边形的面积呢,其实前面的德国数学家已经证明了,用描述的几何的方法。我们这里用极限的方式来证明一下。
在第2部分中,正多边形的面积计算式为:S= P^2/[N*tan(π/N)],因为是增函数,所以当N→ ∞时,S的值趋近极大值,我们来求这个极限值。
LimSN→ ∞=LimN→ ∞P^2/[N*tan(π/N)]=LimN→ ∞P^2*cos(π/N)/[N*sin(π/N)]= P^2* Lim N→ ∞cos(π/N)/ Lim N→ ∞[N*sin(π/N)]= P^2*1/( N*π/N)= P^2/π。
P为周长的一半,对于等周设定中,周长应为2P,用2P的长度围成圆形时,其半径为P/π,其面积为:S圆=π*(P/π)^2= P^2/π,正好为正多边形面积的极限值。
也就是说在欧式空间中,等周封闭平面图形中,圆的面积大于一切正多边形的面积。
至此,对于当初的那些猜想,我们都证明了,但是我们用了很多后面发展出来的知识,比如极限,比如标准圆,比如三角函数,比如不等式,比如微分,海伦定理,一元二次函数等等。这个是实实在在地利用了历史知识积累的优势了。而雅克布的巧思几乎解决了一切问题,这就是思维多样性的魅力。但是他的巧思碰到了更加严谨的存在性的逻辑问题,个人有点为雅克布鸣不平。但雅克布确实跳过了很多我们前面讨论的问题直奔圆这个主题了。
4、 理一理有哪些有用的推论和知识点
推论:
(1) 等周封闭平面多边形中,边长越接近、各顶角角度越接近的情况下面积越大;
(2) 封闭平面多边形中,给定某一条边或某几条相邻的边长,且其余的边长之和为定值时,边长越接近、各顶角角度越接近的情况下面积越大;(帕普斯缺少了这个前提条件);
(3) 封闭平面多边形中,给定某些边长,如果给定的这些边不相邻,其余的边长之和为定值时,未确定的边中,边长分配越接近、形成的顶角度数越接近,面积越大;
(4) 欧式空间中,规则性越高(即各向同性程度越高,或说各方向的属性越相似时),其整体表征出来的数值越大。显然还有其他的推论,暂不推演下去;
(5) 在材料节约、空间容积、力学甚至管理即效能分配方面是否有启示呢?可进一步论证。
知识点:
(1) 标准圆可以将角度和长度在数量上做直观对比;
(2) 海伦公式结合不等式、偏导等可以将一些几何问题转化为数学问题;
(3) 极限计算过程,当无穷大和无穷小同时出现时,要根据无穷大和无穷小的阶数逐步计算靠近,但不要在不明确别的极限值的情况下贸然得出整个极限是无穷大还是无穷小的结论。
(4) 函数之间的关系可能并不是直观想象的那样,比如f(x)=x,g(x)=1/x,二者相乘得f(x)* g(x)=1,从y=1这个固定直线中可以生成一条斜向的直线、两条双曲线;看似复杂的g(x)=1/x,利用一个简单的f(x)=x就可以化繁为简,这些对我们研究自然界,有没有什么启发呢?
版权所有,转发请注明。
,