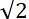在数学的浩瀚海洋中,数字“3”以其独特的魅力和重要性,吸引了无数学者的目光。三的平方,即3的三次方,是9。这个看似简单的算术运算,实则蕴含着深刻的数学意义与广泛的应用。
让我们首先从基础的数学概念谈起。平方是指一个数与其自身相乘的结果,如2乘以2等于4,这是2的平方。那么,三的平方就是3乘以3,得出的结果是9。进一步地,当我们谈论到三的立方(或三次方)时,指的是3乘以自己两次,即3乘以3再乘以3,得出的结果是27。
三的平方之所以引人注目,不仅因为它是一个基本的数学计算,而且还因为“3”本身在数学世界中具有的特殊地位。在自然数中,它是第一个既不是质数也不是合数的数字,因为3不能被除了1和它自己之外的任何其他自然数整除。此外,3还是斐波那契数列中的重要元素,这个著名的数列揭示了许多自然界现象中隐藏的数学规律,如螺旋形态的生长模式等。
在几何学中,三个点可以确定一个平面内的一条直线,而四个点却能构成一个平面四边形。这种由“3”带来的独特结构特性使得三角学成为几何学的一个独立分支。三角形因其稳定性而在工程结构和设计中发挥着重要作用。例如,桥梁和塔架常利用三角形的构造来分散压力,增加结构的稳定性。
在代数学中,三的平方也有着重要的应用。比如,解决三次方程通常需要对方程进行一系列的转换,使其形式化简为易于求解的形式。在处理这类问题时,数学家发展了一系列的理论和技术,其中包括卡丹公式,这是一套用于解三次方程的公式体系。
在物理学中,三的平方同样扮演着关键角色。例如,在量子力学中,粒子的能量级别往往与量子数有关,而这些量子数通常是整数的平方。在电磁学中,库仑定律描述了电荷间的相互作用力,其强度与电荷量的平方成反比,这背后的数学关系也体现了平方在自然规律中的基础地位。
统计学是三的平方另一个不容忽视的舞台。在进行数据分析时,我们常常使用各种模型来描述数据之间的关联性,其中不少模型都涉及到数字3的概念。例如,三个变量之间的相关性可以通过偏相关系数来度量,而这一过程的复杂性随着变量数量的增加而显著提升。
三的平方还出现在经济学的多个角落。市场分析中常用的SWOT分析(优势、劣势、机会和威胁分析)就是一个以三个维度为基础的战略框架,通过这种结构化的分析方法,企业能够更深入地理解自身及竞争环境。
在计算机科学领域,三的平方同样有其用武之地。例如,在数据压缩算法中,利用特定的编码规则减少数据存储空间的需求,这些算法的效率往往与数据的排列组合方式紧密相关,而组合数学正是以数字的排列组合为基础构建起来的学科。
三的平方不仅是一个简单的算术结果,它更是一道通往深刻数学原理和广泛应用领域的门户。无论是在学术研究还是在日常生活的各个方面,三的平方都有着不可忽视的重要性,为我们提供了观察世界的独特视角和解决问题的有效工具。
,