我们学习了加、减、连加、连减的混合运算律,可利用加法的运算定律或连减及加减的混合运算的性质进行简便运算。而乘、除法更有着一些巧妙的简便算法。
乘、除法的巧算方法主要是利用乘、除法的运算定律和运算性质以及积、商的变化规律,通过对算式适当变形,将其中的数转化成整十、整百、整千…的数,或者使这道题计算中的一些数变得易于口算,从而使计算简便。
1.乘法的三个运算定律:
(1)乘法交换律:两个数相乘,交换两个数的位置,积不变。A×B=B×A
(2)乘法结合律:三个数相乘,可以先把前两个数相乘,再与后一个数相乘,或者先把后两个数相乘, 再与前一个数相乘,积不变。 A×B×C=A×(B×C)=A×C×B
(3)乘法分配律:两个数的和(或差)与一个数相乘,可以将这两个数先分别和这一个数相乘,然后再把两个乘积相加(减)。
乘法对加法的分配律:A×(B C)=A×B A×C
乘法对减法的分配律:A×(B-C)=A×B-A×C
乘法对加减法的分配律综合:A×(B C-D)=A×B A×C-A×D。
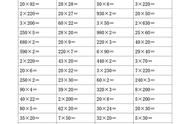
2.计算连乘法时,如果遇到两个乘数相乘可以得到整十、整百、整千……的数,可将它们合并扩整,然后再乘。两数的乘积是整十、整百、整千的,要先乘。为此,要牢记下面这几个特殊的等式
5×2=10: 25×4=100:
125×8=1000; 625×16=10000;
20×5=100; 25×8=200;
27×37=999; 13×77=1001
3.学霸技巧: 乘5 的巧算是减半添0。
例如:26×5=26×10÷2=26÷2×10=13×10=130
142857×7=999999 (记忆方法:6个 9)。
2345679×9=111111111 (记忆方法:9个 1,前面的乘数叫无8数)

【例题1】:计算325÷25
【思路导航】:在除法里,被除数和除数同时扩大或缩小相同的倍数,商不变。利用这一性质,可以使这道计算题简便。
325÷25
=(325×4)÷(25×4)
=1300÷100
=13

【例题2】:计算25×125×4×8
【思路导航】:经过仔细观察可以发现:在这道连乘算式中,如果先把25与4相乘,可以得到100;同时把125与8相乘,可以得到1000;再把100与1000相乘就简便了。这就启发我们运用乘法交换律和结合律使计算简便。
25×125×4×8
=(25×4)×(125×8)
=100×1000
=100000

【例题3】:计算(1)(360 108)÷36 (2)(450-75)÷15
【思路导航】:两个数的和(或差)除以一个数,可以用这个数分别去除这两个数,再求出两个商的和(或差)。利用这一性质,可以使这道题计算简便。
(1)(360 108)÷36 (2)(450-75)÷15
=360÷36 108÷36 =450÷15-75÷15
=10 3 =30-5
=13 =25

【例题4】:计算158×61÷79×3
【思路导航】:在乘除法混合运算中,如果算式中没有括号,计算时可以根据运算定律和性质调换因数或除数的位置。
158×61÷79×3
=158÷79×61×3
=2×61×3
=366
【例题5】:计算下面各题。
(1)123×96÷16 (2)200÷(25÷4)
【思路导航】:这两道题都是乘除混合运算式题,我们可以根据这两道题的特点,采用加括号或去括号的方法,使计算简便。其方法与加减混合运算添、去括号的方法类似,可以概括为:括号前是乘号,添、去括号不变号;括号前是除号,添、去括号要变号。
(1)123×96÷16 (2)200÷(25÷4)
=123×(96÷16) =200÷25×4
=123×6 =8×4
=738 =32