初一动点问题三大公式,初一数学题50道经典题

数轴动点问题是七年级的重难点，涉及数轴、绝对值、整式、方程、绝对值方程、行程问题等诸多知识点。综合性比较强，但有一点不变，就是方程思想，用字母（通常时间t）表示出动点是突破的关键。

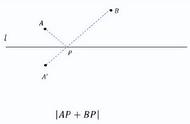
已知数轴上的点A和点B之间的距离为28个单位长度，点A在原点的左边，距离原点8个单位长度，点B在原点的右边。

（1）求两点A、B所对应的数

（2）数轴上点A以每秒1个单位长度出发向左运动，同时点B以每秒3个单位长度的速度向左运动，在点C处追上了点A，求C点对应的数

(3)已知在数轴上点M从点A出发向右运动，速度为每秒1个单位长度，同时点N从点B出发向右运动，速度为每秒2单位长度，，设线段NO的中点为P（O为原点），在运动过程中线段PO-AM的值是否变化？若不变，求其值；若变化，请说明理由。

解析：

(1)A=-8,B=20；

(2)追及问题：B追上A的时间是28÷(3-1)=14(s)，因此可以求C是：C=-8-14×1=-22

(3)t秒后，AM=t,ON=20 2t,所以可得OP=(20 2t)÷2=10 t

∴PO-AM=10 t-t=10

∴PO-AM的值不变，其值是10

已知数轴上有A，B，C三点，分别代表-24，-10，10，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行。甲的速度为4个单位/秒。

（1）问多少秒后甲到A，B，C的距离和为40个单位？

（2）若乙的速度为6个单位/秒，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，问甲，乙在数轴上的哪个点相遇？

（3）在（1）（2）的条件下，当甲到A，B，C的距离和为40个单位时，甲调头返回，问甲、乙还能在数轴上相遇吗？若能，求出相遇点；若不能，请说明理由。

解析：

（1）若甲在AC之间，甲到A 和C的距离和是34，因此只需甲到B的距离为40-34=6即可，而甲在C右边时，甲到A、B、C距离和超过40.

因为AB=14

所以，甲在AB之间，甲B=6，t=（14-6）÷4=2（秒）；甲在BC之间，甲B=6，t=（14 6）÷4=5（秒）

（2）相遇时间：34÷（4 6）=3.4（秒），相遇点：-24 3.4×4=-10.4

（3）由（1）知若甲在AB之间，此时甲B=6，t=2秒，

此时甲乙相距距离是：34-（4 6）×2=14，

乙追上甲时间是：14÷（6-4）=7（秒）

若甲在BC之间，此时甲B=6，t=5秒，此时甲乙已经相遇，因甲速度小于乙速度，故不可能再相遇。

已知数轴上两点A，B对应的数分别为-1，3，点P为数轴上一动点，其对应的数为x。

（1）若点P到点A，点B的距离相等，求点P对应的数。

（2）数轴上是否存在点P，使点P到点A，点B的距离之和为5？若存在，请求出x的值；若不存在，请说明理由。

（3）当点P以每分钟1个单位长的速度从O点向左移动时，点A以每分钟5个单位长的速度向左运动，点B以每分钟20个单位长度的速度向左运动，问它们同时出发，几分钟后P点到点A，点B的距离相等？

解析：

（1）此时P是AB中点，由中点公式可得x=(-1 3)÷2=1

(2)因为AB=3-(-1)=4,因此P不可能在AB之间。

若P在A的左边，则PA距离是：（5-4）÷2=0.5,此时 x=-1-0.5=-1.5

若P在B的右边，则PB距离是：（5-4）÷2=0.5,此时 x=3 0.5=3.5

（3）t秒后。P为-t, A为-1-5t， B为3-20t,

若P为AB中点：-t×2=-1-5t 3-20t, 解得t=2/23

若AB重合：-1-5t=3-20t, 解得t=4/15

已知点A在数轴上对应的数为a，点B对应的数为b，且Ia 4I Ib-1I=0，A，B之间的距离记作AB。

（1）求线段AB的长；

（2）设点P在数轴上对应的数为x，当点PA-PB=2时，求x的值；

（3）若点P在A的左侧，M，N分别是PA，PB的中点，当点P在A的左侧移动时，式子PN-PM的值是否发生改变？若不变，请求其值；若发生变化，请说明理由。

解析：

(1)明显a=-4,b=1,所以AB=5;

(2)因为PA-PB=2，可知PA>PB，所以P在AB之间或B的右边。

若P在B的右边，则PA-PB=5,不可能

若在AB之间，则PA PB=5,PA-PB=2，可得PA=3.5,因此x=-0.5

(3)如下图

PN-PM=(PB-PA)×0.5=5×0.5=2.5

已知数轴上有A、B两点对应数是a,b.满足Ia 1I (b-3)2=0,点P是数轴上一动点，其对应数是m。

（1）求线段AB长；

（2）点C在数轴上对应x,且x是方程2x-4=0.5x 2的解，在AB之间是否存在点P，使得PA PB=PC，若存在，求P对应数，若不存在，说明理由；

（3）在（1），（2）条件下，当点P以每分1个单位的长度从O向左运动，点A以每分5个单位向左运动，点B以每分20个单位向左运动，问它们同时出发几分后，A到P，B距离相等。

解析：

（1）AB=4

(2)解方程得x=4,而PA PB=4,所以PC=4,可得P为0

（3）t分后。P为-t, A为-1-5t， B为3-20t,

若A为PB中点：(-1-5t)×2=-t 3-20t, 解得t=5/11

若PB重合：-t=3-20t, 解得t=3/19