反比例函数四种解析式,反比例函数解析式的确定

点击右上角关注“陈老师初中数理化”分享学习经验，一起畅游快乐的学习生活。

利用几何图形性质求解反比例函数解析式是初二数学的重要题型，本文就例题详细解析这类题型的解题方法，希望能给初二学生的数学学习带来帮助。

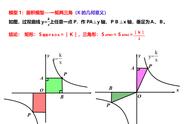
如图，菱形ABCD的顶点A在函数y=3/x(x>0)的图像上，反比例函数y=k/x(k>3,x>0)的图像关于直线AC对称，且经过B,D两点，若AB=2，∠BAD=30°，求k的值。

解题过程：

连接OA、AC，过点A作AM⊥x轴于点M，过点B作BN⊥x轴于点N，过点A作AE⊥BN于点E

根据双曲线的轴对称性和题目中的条件：反比例函数y=k/x(k>3,x>0)的图像关于直线AC对称，则点A、C、O在一条直线上，∠MOA=45°；

根据菱形的性质和题目中的条件：四边形ABCD为菱形，则AC平分∠BAD，即∠BAC=∠BAD/2；

根据题目中的条件和结论：∠BAD=30°，∠BAC=∠BAD/2，则∠BAC=15°；

根据题目中的条件和结论：AM⊥x轴，∠MOA=45°，则∠OAM=45°；

根据等角对等边性质和结论：∠MOA=∠OAM=45°，则OM=AM；

设AM=a

根据题目中的条件和结论：AM⊥x轴，OM=AM=a，则点A的坐标为(a,a)；

根据题目中的条件和结论：点A在函数y=3/x(x>0)的图像上，A(a,a)，则a=√3；

根据结论：OM=AM=a，a=√3，则OM=AM=√3；

根据结论：∠OAM=45°，∠BAC=15°，则∠BAM=120°；

根据题目中的条件：AM⊥x轴，BN⊥x轴，AE⊥BN，则∠AMN=∠BNM=∠AEN=90°；

根据矩形的判定和结论：∠AMN=∠BNM=∠AEN=90°，则四边形AMNE为矩形；

根据矩形的性质和结论：四边形AMNE为矩形，则AE=MN，AM=EN，∠MAE=90°；

根据结论：∠BAM=120°，∠MAE=90°，则∠BAE=30°；

根据直角三角形的性质和结论：AE⊥BN，∠BAE=30°，AB=2，则BE=AB/2=1；

根据勾股定理和结论：AE⊥BN，AB=2，BE=1，则AE=√3；

根据结论：AE=MN，AM=EN，AE=√3，AM=√3，则EN=MN=√3；

根据结论：OM=√3，MN=√3，EN=√3，BE=1，则ON=OM MN=2√3，BN=BE EN=√3 1；

根据结论：BN⊥x轴，ON=2√3，BN=√3 1，则点B的坐标为(2√3,√3 1)；

根据题目中的条件和结论：点B在函数y=k/x(x>0)的图像上，B(2√3,√3 1)，则k=6 2√3。

解决本题的关键是根据反比例函数图像的轴对称性质添加辅助线，利用菱形和轴对称性质得到角度间的数量关系，根据直角三角形性质和勾股定理得到线段间的数量关系，就可以求得反比例函数图像上的点坐标，进而求得函数解析式。