一般地,形如 y = k/x ( k是常数, k ≠ 0 ) 的函数叫做反比例函数。
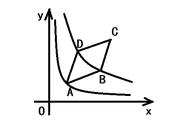
二、反比例函数的图象和性质:1、形状:图象是双曲线。
2、位置:(1)当k>0时,双曲线分别位于第一、三象限内;(2)当k<0时, 双曲线分别位于第二、四象限内。
3、增减性:(1)当k>0时,在每个象限内,y随x的增大而减小;
(2)当k<0时,在每个象限内,y随x的增大而增大。

4、变化趋势:双曲线无限接近于x、y轴,但永远不会与坐标轴相交。
5、对称性:(1)对于双曲线本身来说,它的两个分支关于直角坐标系原点中心对称;
(2)对于k取互为相反数的两个反比例函数(如:y = 6/x 和y = -6/x)来说,它们是关于x轴,y轴对称。
三、反比例函数中比例系数k的几何意义:1、反比例函数与矩形面积:
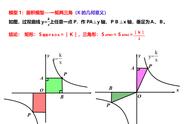
若P(x,y)为反比例函数y=k/x(k≠0)图像上的任意一点如图1所示,过P作PM⊥x轴于M,作PN⊥y轴于N,求矩形PMON的面积.

分析:
S矩形PMON=PM·PN=│y│·│x│=│xy│
∵y=k/x,∴ xy=k,∴S =│k│.
2、反比例函数与三角形面积:
若Q(x,y)为反比例函数y=k/x(k≠0)图像上的任意一点如图2所示,过Q作QA⊥x轴于A(或作QB⊥y轴于B),连结QO,则所得三角形的面积为:S△QOA=│k│/2(或S△QOB=│k│/2).

说明:以上结论与点在反比例函数图像上的位置无关.
求两个函数图像的交点,往往把两个函数的表达式联立组成方程组,方程组的解就是交点的坐标。
(1)正比例函数y=k₁x(k₁≠0)与反比例函数y=k₂/x(k₂≠0),当k₁与k₂同号时,正比例函数图像与反比例函数图像有两个交点,即对应方程组的解,且两个交点关于原点对称;当k₁与k₂异号时,两个函数图像没有交点。
(2)一次函数y=k₁x b(k₁≠0)与反比例函数y=k₂/x(k₂≠0)图像交点个数有三种情况:1个,2个或0个。因为两个函数表达式联立组成的方程组可化成一个二次方程,所以两个函数交点个数由这个一元二次方程实数解的个数来决定。注意:求出一元二次方程的解后,要注意判断是否为增根。

关于反比例函数图像与一次函数图像的交点的问题,我会在后面详细分析讲解,欢迎大家关注。