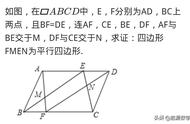
浙江省绍兴市中考曾经有这样一道题:
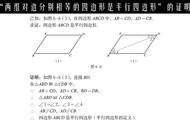
小敏不慎将一块平行四边形玻璃打碎成如图1的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )

A.①,② B.①,④ C.③,④ D.②,③
解答此题的关键是了解平行四边形全等的判定.那么,两个平行四边形全等究竟需要哪些条件呢?
根据平行四边形的性质“两组对边分别平行且相等,两组对角分别相等,两条对角互相平分”及图形全等的定义,可得平行四边形全等的判定方法有如下几种:
方法一:被一条对角线分成的三角形中有一个对应全等的两个平行四边形全等.

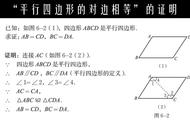
如图2,在□ABCD和□A/B/C/D/中,如果△ABC≌A/B/C/,那么□ABCD≌□A/B/C/D/;
方法二:一组邻边和一个内角对应相等的两个平行四边形全等.

如图3,在□ABCD和□A/B/C/D/中,如果AB=A/B/,BC=B/C/,∠A=∠A/或∠B=∠B/,那么□ABCD≌□A/B/C/D/;
方法三:一组邻边和一条对角线对应相等的两个平行四边形全等.
方法四:一边和两条对角线对应相等的两个平行四边形全等.
根据上述判定方法可知确定平行四边形的条件有三种,分别是:
(一)一组邻边的长和一个角的度数;
(二)一组邻边和一条对角线的长;
(三)一边和两条对角线的长.
对于上述问题,如果带去①②,只能确定一边的长和一个角的度数,所以不能确定平行四边形;如果带去①④,只能确定一个角的度数;如果带去③④,也只能确定一边的长和一个角的度数;如果带去②③,将②③按弧线拼接后延长相邻的两边可以确定一组邻边的长和一个角的度数,从而可以确定平行四边形.故选D.
,