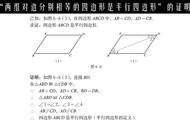
【解析】(1)因为AE∥BC,所以∠A=∠B.又因AD=BF,所以AF=AD DF=BF FD=BD,又因AE=BC,所以△AEF≌△BCD.
(2)因为△AEF≌△BCD,所以∠EFA=∠CDB,所以EF∥CD.
【点评】根据平行寻求全等的条件,由三角形全等的性质证两直线平行.
利用平行四边形的性质求面积
例4.如图,在□ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,
求证:S△ABF=S□ABCD.

【解析】∵四边形ABCD为平行四边形,∴AD∥BC.
∵E是DC的中点,∴DE=CE.∴△AED≌△FEC.∴S△AED =S△FEC.
∴S△ABF =S四边形ABCE S△CEF =S四边形ABCE S△AED =S□ABCD
会根据条件选择适当方法判定平行四边形
例5.如图,在□ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )

A.OE=OF B.DE=BF
C.∠ADE=∠CBF D.∠ABE=∠CDF
【分析】虽然判别平行四边形可从“边、角、对角线”三个角度来考虑,但此例图中已有对角线,所以最适当方法应是“对角线互相平分的四边形为平行四边形”.
能利用平行四边形的性质进行计算
例6.如图,在□ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC BD=_______.

【分析】本例解题依据是:平行四边形的对角线互相平分,先求出AO BO=9,再求得AC BD=18.
持续关注我们,后期将分享更多相关学习资料,以下目录提前预览: