堆是一种数据结构,它是一颗完全二叉树。其中每个父节点的值都小于或等于其所有子节点的值。整个堆的最小元素总是位于二叉树的根节点。python的heapq模块提供了对堆的支持。堆数据结构最重要的特征是heap[0]永远是最小的元素
区分堆(heap)与栈(stack):
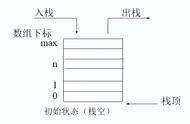
堆与二叉树有关,像一堆金字塔型泥沙;而栈像一个直立垃圾桶,一列下来。
堆常用方法import heapq
import random
heap = []
# 数据加入堆中
for i in range(10):
heapq.heappush(heap, random.randint(1, 100))
print(f"heap: {heap}")
# 弹出并返回 heap 的最小的元素,保持堆的不变性。如果堆为空,抛出 IndexError 。使用 heap[0] ,可以只访问最小的元素而不弹出它
pop = heapq.heappop(heap)
print(f"pop min: {pop}")
# 将 item 放入堆中,然后弹出并返回 heap 的最小元素。该组合操作比先调用 heappush() 再调用 heappop() 运行起来更有效率。
pop_push = heapq.heappushpop(heap, 200)
print(f"pop and push: {pop_push}")
# 将list x 转换成堆,原地,线性时间内
heapq.heapify(heap)
print(type(heap), heap)
# 弹出并返回 heap 中最小的一项,同时推入新的 item。 堆的大小不变。 如果堆为空则引发 IndexError
s = heapq.heapreplace(heap, 201)
print(f"pop:{s}, heap: {heap}")
# 将多个已排序的输入合并为一个已排序的输出
# heapq.merge(*iterables, key=None, reverse=False)
# 类似于 sorted(itertools.chain(*iterables)) 但返回一个可迭代对象,不会一次性地将数据全部放入内存,并假定每个输入流都是已排序的(从小到大)
li = [1, 2, 3, 5]
li1 = [2, 3, 5, 6]
ll = heapq.merge(*(li, li1), reverse=False)
print(f"heap merge: {[t for t in ll]}")
# 查询堆中的最大元素,n表示查询元素个数
top_3 = heapq.nlargest(3, heap)
print(f"heap top3: {top_3}")
# 查询堆中的最小元素,n表示查询元素的个数
min_3 = heapq.nsmallest(3, heap)
print(f"heap min3: {min_3}")
print(f"heap: {heap}")结果

- 合并K个升序链表
给你一个链表数组,每个链表都已经按升序排列。 请你将所有链表合并到一个升序链表中,返回合并后的链表。
import heapq
from typing import List, Optional
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class Solution:
def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
# 堆排序
heap = []
for i in lists:
while i:
heapq.heappush(heap, i.val) # 值加入heap
i = i.next
new_node = move_node = ListNode()
while heap:
move_node.next = ListNode(heapq.heappop(heap)) # 每次弹出最小的值
move_node = move_node.next
return new_node.next,