解答第二问时,我们还得回到题目中,抓住题目中出现的关键字眼来解题。题目中说所有木块与木板之间的动摩擦因素相同,也就是说所有木块做匀减速的加速度相等,也就是说所有木块的速度减少量是相等的,又因为所有木块没有相互碰撞,这句话更充分说明了木块的速度减少量时相等的。

第1号木块与木板相对静止时,木块与木板的速度是相同的,设此时的速度为V1,该木块速度的减少量△V=V0-V1,在这段时间内,所有木块与木板间的速度减少量都为△V。由动量守恒定律可知,所有的木块动量的减小量等于木板动量的增加量,故而有MV1=nm(V0-V1),解得V1=V0/2。
解答本题中的第二问是灵活的运用了动量守恒定律。

在解答第三问时,我们首先得弄明白一件事,也就是说,木块的最小速度为多大呢?这时我们就要从木块的运动规律上来说,木块在木板上做匀减速运动,通常情况下,速度为零为任何运动物体的最小速度,但是由于木板和水平面没有摩擦力,故而木板也会随着木块一起运动,也就是说,第K号木块的最小速度跟此时木板的速度相等,也就是木块与木板处于将对静止状态。

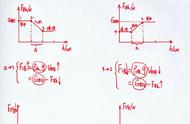
由第二问可知,此时从第1、2、3、4……K号木块与木板的速度均为Vk,而从第k 1,k 2……n号木块动量的减小至共为(n-k)m(kV0-Vk),由动量守恒定律可得m(1 2 3 4…… K)V0 ((n-k)m(kV0-Vk)=(km M)Vk,解得Vk=k(2n 1-k)V0/4n,其中n>k。
解答第三问同样灵活的运用了动量守恒定律,即在第K号木块时,左边式子的动量减少量等于右边式子的动量增加量。
,