(bluehouse456 全文整理)
同学们大家好,很高兴和大家一起学习今天的内容。
和我们一同上课的还有小英、小丁和欢欢,欢迎大家的到来,让我们开始今天的学习吧。
上课之前,我们先回忆一下。
大家都学过哪些图形?
有。
长方形。
正方形。
三角形和平行四边形。
你能给它们分分类吗?
欢欢说。
三角形有三条边,分一类,其他图形有四条边分一类,这是根据边的数量分得的结果。
再来看看四边形中的长方形、正方形和平行四边形。
它们有什么共同的特点?
小英。
它们都有四条边,对边相等,还有四个角。
都是有两组对边,分别平行。
请你猜一猜。
除了有两组对边分别平行的四边形以外。
还会有怎样的四边形?
会不会有一组对边平行,一组对边不平行的四边形呢?
如果四边形只有一组对边平行,请你想象一下是什么样子的。
生活中你能找到这样的图形吗?
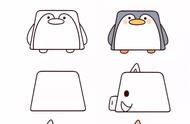
我在梯子上见过。
我在花盆上见过。
我在跳江上见过。
他们是不是只有一组对边平行呢?让我们验证一下。
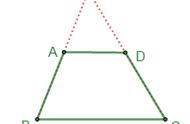
这一组对边平行。
另一组对边如果延长出去后,会出现相交的情况,看来只有一组对边平行。
这个图形。
也是一组,对边平行。
另一组对边不平行。
同样。
最后一幅图。
也是这样的特点,一组对边平行,另一组对边不平行。
这三个图形都是一组对边平行,另一组对边不平行,我们把只有一组对边平行的四边形叫做梯形。
但是在刚刚给出的这些图形中,没有梯形。
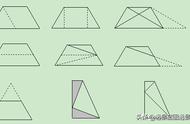
你能通过画一画、减一减得到题型吗?请大家赶快动手试一试吧。
接下来的时间就交给你们。
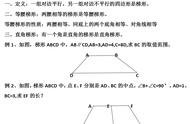
那我们来看看同学们的作品吧。这是小英的,我是用三角形制作的,三角形只有三条边,也没有平行线,借助前面学过的画平行线的方法,找到一条与底边平行的线,然后剪下来就得到了梯形。
当然也可以根据另外两条边分别找平行线去剪,是不是很厉害?
欢欢又是如何得到的呢?让我们一起来听听他的介绍。
我是利用平行四边形剪出的,梯形有两组平行线,而梯形只有一组需要破坏一,所以我这样从顶点斜着一点,去掉一个角就可以得到梯形了。如果从里面斜着点可以得到两个梯形呢?你也可以试一试。
再来看看小丁的想法。
我是用长方形剪的,方法和前一位同学的很像,也要破坏掉一组平行线,从顶点斜着剪,可以剪出一个梯形和一个三角形。
如果从中间斜着减,可以得到两个梯形。
利用正方形减的方法也一样,斜着减可以得到一个或者两个梯形。
大家的方法都很好,有的是得到了一个题型,有的得到了两个。不论怎样,我们的目的只有一个,就是要得到只有一组对边平行的四边形,也就是梯形了。
接下来让我们了解一下梯形的各部分名称。
这一组互相平行的边分别叫做上底和下底。
不平行的这一组边叫做腰。
夹在两平行线间的垂线段就是梯形的高。
梯形有多少条高?
老师,通过您的演示,我觉得应该有无数条高。
是的,只要是加在两条平行线间的垂线段,就都是它们的高。
如何确定下面这两个梯形的各部分名称呢?哪位同学愿意说一下?
小丁水平方向的这一边,上面的是上底。
下面的是下底。
左右两边的是腰。
夹在两底之间的垂线段叫做高。
但是右边的图,我就不知道如何确定上底和下底了。
这样放置的梯形,左右两条平行线,上下底可以随意认命。
左边的如果是上底,右边的就是下底,反过来也可以。
不平行的这两条边,自然就是腰了。
加在中间的垂线段就是高。
请大家观察一下同学们制作的这些梯形,有哪些梯形有特殊的地方?
让我们听听小英的想法。
我对折了一下,发现这两个梯形的腰都相等。
通过对折,小英有了发现,欢欢还有补充。
这个梯形是轴对称图形吧?
小丁,又有什么发现呢?
我是用长方形或正方形剪的,发现剪出的梯形上面都有两个直角。
带着同学们的发现,让我们一起来看一看。
两腰相等的梯形叫做等腰梯形。
有一个角是直角的梯形叫做直角梯形。
等腰梯形和直角梯形都是特殊的梯形,同学们有什么问题吗?
小英,说说你的想法,为什么这里说有一个角是直角?
刚才小丁同学剪出的直角梯形都是有两个角是直角,只有一个角是直角,可以吗?
这是一个好问题,让我们看看同学们验证的情况吧。
我画了好几个梯形。
都发现,如果一个角是直角。
那么另一个角肯定也是直角。
如果不画成直角,剩下这两条边就不平行了。
感兴趣的同学们,课下可以试一试。
同学们,现在你们能不能根据要求画出梯形呢?
这是电子图,电子图上水平和竖直方向相邻两点之间的距离是一厘米。
请你在这个点子图上画出三个不同的梯形,但是三个梯形的一条底都是四厘米,高都是两厘米。
听清要求了吗?好,请大家拿出尺子和笔,开始吧。
让我们一起看看同学们的作品。这是欢欢画出的三个梯形,都有一条底是四厘米,高是两厘米,只不过有的是上底为四厘米,有的是下底为四厘米,但全都符合条件。
其实啊,还有些同学在画的过程中还找到了规律呢,让我们一起来看看。
这是小鹰的发现,我是这样画的,先画了一条四厘米的线段作为下笔,然后向上找到距离两厘米的这条线。
在上面画一厘米的线段,再连接左右两边的线。
后面的图,我是把上面的这条线段向右移动一格。
就得到了第二个梯形。
再向右移动一格。
就得到了第三个梯形,也可以向左移动,这样就可以画出很多个不一样的梯形了。
小鹰是固定了下底和高,通过移动上底得到了不同的梯形,这个方法非常好。
小英用这种方法画出的梯形,虽然样子不太一样,但是它们有没有相同的地方呢?
欢欢说,他们的上底,下底和高都相等。
虽然他们的样子长得不太一样。
但是他们的上底、下底和高分别都相等。
再来看看小丁找到了怎样的规律。
我是把四厘米的线段当成上底。
然后向下两厘米处找到下底的位置。
然后画出一厘米作为下底。
接下来我固定好这一点,另外一点向右移动。
就可以画出不同的梯形了。
小丁是通过移动最下面一点画出来不同的梯形,欢欢有什么问题呢?
可是再往下移动一个点是不是就不行了呢?我沿着你的思路想了一下,感觉变成平行四边形了。
这是一个好问题。
如果右下角这一点继续往右移动,你能想象出所出现的图形的样子吗?现在是梯形。
梯形。
梯形。
平行四边形。
再向右移动,还是梯形吗?
我感觉它既不像平行四边形,也不像梯形。
我觉得它还是梯形,因为它仍然有一组对边平行。
谢谢你,我明白了。同学们在讨论中相互启发,抓住梯形只有一组,对边平行去思考,非常好。
右下角的点如果反过来向左移动。
梯形。
平行四边形。
梯形。
最后变成了三角形。
大家的讨论特别有意义,在动态变化的过程中,还要注意区分梯形与平行四边形和三角形的不同。
截止到现在,我们认识的四边形有长方形、正方形、平行四边形和梯形。
如果用椭圆表示四边形这个大家族,你能表示出长方形、正方形、平行四边形和梯形之间的关系吗?
拿出学习单思考一下,然后把你的想法在椭圆形中表示出来吧。
让我们一起看看小丁的想法,我是这样表示的,正方形、长方形和平行四边形都有两组对边分别平行,所以分一类,梯形只有一组对边平行,所以分一类。
欢欢有不同的意见。
原来学过的正方形是特殊的长方形,长方形是特殊的平行四边形,它们之间不应该是并列关系吧?
再来看看欢欢的想法,我是这样想的,正方形是特殊的长方形,平行四边形是特殊的梯形。
欢欢,这样想可以吗?
小丁说。
我不同意梯形是只有一组对边平行,平行四边形是两组对边分别平行,没有包含关系。
是呀,平行四边形不属于梯形。
通过刚才的讨论,小英很受启发,让我们听听他的想法。
左边的都是两组对边平行,右边的梯形只有一组对边平行。
欢欢补充道,这样平行四边形与长方形、正方形的关系就合理了。
按照这样的想法,我们能再梳理一下,在四边形中圈出一类只有一组对边平行的四边形,叫做梯形。
然后再分出有两组对边分别平行的四边形,叫做平行四边形。在平行四边形中包括长方形,长方形是特殊的平行四边形,长方形中又可以分出一类正方形,正方形是特殊的长方形。
这样就形成了四边形之间的关系结构图。
通过今天的课,你有哪些收获?我认识了梯形。
我找到了梯形和其他图形之间的关系。
我能表示出他们的关系。
带着你们的收获,相信你们能够去探索更多更复杂的图形。
今天我们学习的内容在数学书第66页。
课后请同学们完成数学书第66页的做一做一。
还有第68页的第六题。
今天这节课,我们就先学习到这里。
,