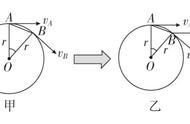
13.如图8所示,甲、乙两物体自同一水平线上同时开始运动,甲沿顺时针方向做匀速圆周运动,圆半径为R;乙做自由落体运动,当乙下落至A点时,甲恰好第一次运动到最高点B,求甲物体做匀速圆周运动的向心加速度的大小.(已知重力加速度为g)

1.B [做匀速圆周运动的物体的加速度就是向心加速度,其方向指向圆心,B正确.]
2.D [物体做匀速圆周运动的向心加速度与物体的线速度、角速度、半径有关.但向心加速度与半径的关系要在一定前提条件下才能成立.当线速度一定时,向心加速度与半径成反比;当角速度一定时,向心加速度与半径成正比.对线速度和角速度与半径的关系也可以同样进行讨论.正确选项为D.]
3.D [由题意知,木块做匀速圆周运动,木块的加速度大小不变,方向时刻指向圆心,D正确,A、B、C错误.]
4.CD [由a=Rω2,v=Rω可得ω= ,v=,a=ωv,即A、B错误,C正确;又由T=与ω= 得T=2π,即D正确.]
5.A [角速度为ω==π rad/s,A错误;转速为n==0.5 r/s,B正确;半径r== m,C正确;向心加速度大小为an==4π m/s2,D正确.]
6.AB [因为a=ω2R,所以小物块运动的角速度为ω==2 rad/s,周期T==π s,选项A、B正确;小物块在 s内转过,通过的位移为 m,在π s内转过一周,通过的路程为2π m,选项C、D错误.]
7.B [a、b两玩具车的线速度之比va∶vb=sa∶sb=3∶4,角速度之比ωa∶ωb=θa∶θb=2∶3,故它们的向心加速度之比aa∶ab=vaωa∶vbωb=1∶2,B正确.]
8.A [A、B两点随球体一起绕轴O1O2转动,转一周所用的时间相等,故角速度相等,有ωA=ωB=ω,选项A正确.A点做圆周运动的平面与轴O1O2垂直,交点为圆心,故A点做圆周运动的半径为rA=Rsin 60°;同理,B点做圆周运动的半径为rB=Rsin 30°,所以A、B两点的线速度分别为:vA=rAω=Rω,vB=rBω=Rω,显然vA>vB,选项B错误.A、B两点的向心加速度分别为:aA=rAω2=Rω2,aB=rBω2=Rω2,显然,A、B两点的向心加速度不相等,且它们的向心加速度方向指向各自平面的圆心,并不指向球心,故选项C、D错误.]
9.C [同轴转动,C、E两点的角速度相等,由an=ω2r,有=2,即anC=2anE;两轮边缘点的线速度大小相等,由an=,有=,即anC=anD,故选C.]
10.CD [由题意可知,b、c、d是固定在同一轮轴的两轮上的点,因此ωb=ωc=ωd,a、c为用皮带连接的两轮边缘上的点,皮带不打滑时有va=vc,故选项C正确;由角速度与线速度的关系v=ωr并结合题中所给各点的半径,易得ωa=2ωc=2ωb=2ωd及va=2vb,由此排除A、B两选项;由向心加速度an=ω2r可推得ana=and,则选项D正确.]
11.0.24 m/s2 0.04 m/s2
解析 压路机匀速行驶时,vB=vA,
由an=,得==2
得aB=2aA=0.24 m/s2
又ωA=ωC,由an=ω2r,得==
得aC=aA=0.04 m/s2.
12.50 m/s2,方向竖直向上 0
解析 运动员经圆弧滑到C点前做圆周运动.因为不计各种阻力,故经过C点之前的瞬间,运动员只在竖直方向上受力,只有向心加速度.由an=得运动员到达C点前的瞬时加速度a1= m/s2=50 m/s2,方向竖直向上.运动员滑过C点后,进入水平轨道做匀速直线运动,故加速度a2=0.
13.π2g
解析 设乙下落到A点所用时间为t,
则对乙,满足R=gt2,得t= ,
这段时间内甲运动了T,即T= ①
又由于a=Rω2=R②
由①②得,a=π2g.