第一章 :方周率
一、根据正方形的原理,它是由(点线边)组成。
找出正方形的规律和共同点
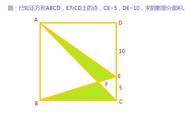
如:已知,在正方形边长为1的情况下,求对角线。
根据勾股定理,可知,1平方+1平方=2 √2=1.414……
所以对角线=1.414……
如:已知正方形边长为2 求对角线。
根据来回循环定理
2×√2=2.828……
所以对角线=2.828……
如:己知,正方形边长为3 求对角线
根据来回循环定理
3×√2=4.242……
所以对角线=4.242……
依次类推为一样的道理
综合以上原理得出规律定律和共同点。
规律为√2 为正方形的规律,1.414……为正方形规律的共同点,定律:为任何一个正方形边长×√2=对角线。所以1.414……为正方形周率,简称为方周率。
这就是根据正方形的性质和原理,由(点线边)一来一回,经过组合重叠叠加来回循环定理而推算出来的结果,简称为(来回循环定理)。
第二章 :正长方形
一、找出正长方形的规律和共同点。
如:正长方形的长(边长)为1 的情况下,求对角线。
根据勾股定理
已知:1平方+0.5平方=1+0.25=1.25 √1.25=1.118……
所以对角线=1.118……
如:正长方形长(边长)为2
根据来回循环定理
2×√1.25=2.236……
所以对角线=2.236……
如:正长方形长(边长)为3
根据来回循环定理
3×√1.25=3.354……
所以对角线=3.354……
依次类推为一样的道理
综合以上原理推算,得出规律定律和共同点。定律:任何一个正长方形长(边长)×√1.25=对角线。
规律:√1.25为正长方形的规律。
这个规律的共同点为1.118……为正长方形规律的共同点。
这个共同点为正长方形周率,简称为长周率。
所以1.118……为长周率
这就是根据正长方形的性质和原理,由(点线边)一来一回
经过组合重叠叠加来回循环定理而推算出来的结果。简称为(来回循环定理)。
第三章 : 正三角形
一、根据正三角形的原理,它是由(点线边)组成。
找出正三角形的规律和共同点
1、如:己知,正三角形边长为1 的情况下,求中线。
可知,根据勾股定理
1平方—0.5平方=1—0.25=0.75 √0.75=0.866……
所以中线=0.866……
2、如:已知正三角形边长为2求中线。
根据来回循环定理
2×√0.75=1.732……
所以,中线=1.732……
3、已知正三角形边长为3,求中线。
根据来回循环定理
3×√0.75=2.598……
所以中线=2.598……
4、已知,正三角形边长为4
求中线
根据来回循环定理
4×√0.75=3.464……
所以,中线=3.464……
综合以上得出规律定律和共同点。
定律:任何一个正三角形边长× √0.75=中线。
规律:√0.75为正三角形的规律,这个规律的共同点为3.464……
所以3.464……为正三角形周率简称为三角周率。
这就是根据正三角形的性质和原理,
由(点线边)组成。
由点线边一来一回经过组合,
重叠叠加来回循环定理而推算出来的结果。简称为(来回循环定理)。
第四章 : 什么叫来回循环定理
一、如:正方形边长为1的情况下,求对角线。
根据勾股定理
1平方+1平方=2 √2=1.414……
对角线=1.414……
二、 1+1就等于2条边相加等于2,为组合叠加。
从2条边再到求对角线为多少,就为2条边上各为1(代表1个点)然后再到对角线(代表线)为(来回)所得出来的数据同样为点,这就形成(点线边)一来一回经过组合重叠叠加来回循环定理。由(点)为边上为1(为1个点)(线)为对角线,(边)为4条边,这就叫(点线边)来回循环定理。三、如:周长为4,求对角线
已知,周长为4
可知,√4=2 √2=1.414……
所以对角线=1.414……
边长求对角线=1.414……
这就形成重叠,边长和周长求出对角线都为一样的数据。其实就是一个正方形经过对角线,折叠成2个相等的三角形。把它放开又是一个原来的正方形,这就叫来回组合重叠叠加。这就是来回循环定理的性质原理和它的函义。
小数点后保留3位数字。
最后,希望大家观看以后,提出宝贵的意见,多多关注和支持,多多推荐给更多的朋友。 谢谢!
另外,我还有很多个作品,如方周率,长周率,周率论,三角周率,论述四周率等等,希望大家在百度点击查看。