(2023-04-03 )
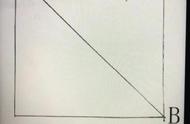
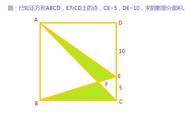
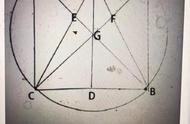
头条上看到一个非常不错的小学六年级数学几何题,如何解?

解1:
正方形的对角线=圆的半径。
而正方形的对角线是其边长的√2倍。
正方形的边长=√30
正方形的对角线=2√15
圆的面积=(2√15)²π=60π
四分之一圆面积=15π
阴影部分的面积=15(π-2)(㎝²) (或进一步得出=15π-30)
点评:以上解法,得分25%。恭喜能用熟悉的知识找出一般解决问题的思路。
解2:
这题无解,缺少条件,A点不一定是圆心。
点评:以上解法,得分50%。恭喜能用熟悉的知识找出题目所存在的缺陷(或陷阱),并有质疑、挑战权威的勇气。
解3:
这题缺少条件,无解。
如果BE=FD,或A为圆心,则有:
正方形的对角线=圆的半径。
而正方形的对角线是其边长的√2倍。
正方形的边长=√30
正方形的对角线=2√15
圆的面积=(2√15)²π=60π
四分之一圆面积=15π
阴影部分的面积=15(π-2)=15π-30(㎝²)
点评:以上解法,得分75%。能用熟悉的知识找出题目所存在的缺陷(或陷阱),有质疑、挑战权威的勇气,并能给出补救性的解决办法。
解4:
这题缺少条件,无解。
一个四分之一半圆,半圆弧上小于45度角的任意一点,都可以做一条到半圆的底边(半径)的垂线,以垂线为边画出正方形。只有45度角上的点形成的正方形的对角线即这个半圆的半径,其他均不是。
题目应完善为:四分之一半圆扇形内一正方形面积为30,求正方形以外阴影面积。(明确是扇形是关键,扇形定义是到圆心的,不是扇形则无解)。
完善之后有以题解:
正方形的对角线=圆的半径。
而正方形的对角线是其边长的√2倍。
正方形的边长=√30
正方形的对角线=2√15
圆的面积=(2√15)²π=60π
四分之一圆面积=15π
阴影部分的面积=15(π-2)=15π-30(㎝²)
点评:以上解法,得分100%。能用熟悉的知识找出题目所存在的缺陷(或陷井),有质疑、挑战权威的勇气,其论证过程表述清晰易理解,能完善题目并给出解答。
数学学习中应鼓励学生养成以下几种习惯:
- 鼓励用更多方法去解题。
- 鼓励以用最基本的知识点进行推导解释和质疑(这点可多看下《几何原本》)。
- 鼓励去做完善者,而不仅仅是一个质疑者。因为以后的工作更需要一个完善者。

此题目,目前适合做为综合引导用,能锻炼数学的解题思维、语文的论证表述的综合能力,还有培养勇于挑战和做个完善者的特质。暂不适合做普通试题,普通试题应标准无错漏,才便于公平公正的卷面评分。
可以看看原文链接下的相关评论就知道做个挑战者和完善者有多难:
https://www.toutiao.com/w/1760486121849864/?log_from=93f947fa94bf5_1679091227627
约有60%的人在努力解题;(不能提出质疑,用已有知识去尽量解决问题)
约有10%的人在发表无意义内容。
约有10%的人提出质疑;(能从已有知识发现问题,并勇于提出挑战)
约有18%的人对质疑发起论战(以传统思维、不完善的知识,去维护出题的权威);
约有2%的人能说清问题本质,并给出完善,从而让人无可论战。
评论中相关不完善的知识点易导致思维进行传统陷阱,都是可以设计一下,提出和学生们一起探讨以加强其对基础知识的理解:
- 正方形都是直角,那么A肯定是圆心。
- 连接AC,AC就是半径,正方形对角线正好是圆半径。
- 根本不需要用到扇形,简单送分题而已。
人工智能时代已来临,学习需要与时俱进。人工智能是基于数据喂养,在创新上仍有局限性。未来教育出来的人才,是需要与人工智能互补的,否则就容易被人工智能所替代(重复性的工作)。和人工智能比记忆、比知识的全面性、比翻译无疑是可笑的,过多的投入在知识考点记忆、语言类学习将是一种教育浪费。未来的人才,一定是创新性人才,一定是利用综合能力解决问题的人才。培养终身学习能力、创新能力、适应能力、团队协作能力和领导力,跨学科、解决复杂问题的能力才能更显人类的优势。
此为沉墨的猫之原创,分享的内容可用之,但请尊重我的著作权益。理工男,喜欢讨论解决问题(含教育等)。