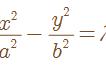欢迎关注公众号:总结数学。免费领取更多精品资料。
题型一:双曲线的定义及应用
双曲线定义的应用策略
(1)根据动点与两定点的距离的差判断动点的轨迹是否为双曲线.
(2)利用双曲线的定义解决与双曲线的焦点有关的问题,如最值问题、距离问题.
(3)利用双曲线的定义解决问题时应注意三点:①距离之差的绝对值;②2a<|F1F2|;③焦点所在坐标轴的位置.
题型二:双曲线的焦点三角形
题型三:双曲线的渐近线及应用
题型四:双曲线的方程
题型五:双曲线的离心率及范围
求椭圆离心率的值(范围),其方法为:
(1)定义法:根据条件求出a,c,直接利用公式e=a(c)求解.
(2)方程法:根据条件得到关于a,b,c的齐次等式(不等式),转化为关于a,c的齐次等式(不等式),然后将该齐次等式(不等式)两边同时除以a或a2转化为关于e或e2的方程(不等式),解方程(不等式)即可得e(e的取值范围).
(3)根据题目条件中的几何信息,建立方程或者不等式。
离心率的范围问题:在寻找不等关系时通常可从以下几个方面考虑:
(1)题目中某点的横坐标(或纵坐标)是否有范围要求:例如椭圆与双曲线对横坐标的范围有要求。如果问题围绕在“曲线上存在一点”,则可考虑该点坐标用
表示,且点坐标的范围就是求离心率范围的突破口
(2)若题目中有一个核心变量,则可以考虑离心率表示为某个变量的函数,从而求该函数的值域即可
(3)通过一些不等关系得到关于的不等式,进而解出离心率
题型六:双曲线与直线的位置关系