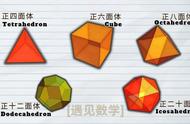
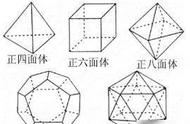
只有五种多面体是正多面体。
证明如下:设正多面体每个顶点有m条棱,每个面都是正n边形,多面体的顶点数是V,面数是F,棱数是E。因为两个相邻面有一公共棱,所以

因为两个相邻顶点有一公共棱,所以

又因多面体的Euler定理,得V F-E=2,从上面三式可得

要使得上面的式子成立,必须满足2m 2n-mn>0,即1/m 1/n>1/2。因为m≥3,所以

只有五种多面体是正多面体。
证明如下:设正多面体每个顶点有m条棱,每个面都是正n边形,多面体的顶点数是V,面数是F,棱数是E。因为两个相邻面有一公共棱,所以

因为两个相邻顶点有一公共棱,所以

又因多面体的Euler定理,得V F-E=2,从上面三式可得

要使得上面的式子成立,必须满足2m 2n-mn>0,即1/m 1/n>1/2。因为m≥3,所以













Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.