草图是无法找到解的,说明m=5,n=4,不可能画出整个球面上的均分点。同理,m=5,n≥5,均不可能。
至于为什么无解呢?还是因为主圆最上面象限点与阵列点之间的距离小于副圆的半径。因此不可能有解。
综上我们使用solidworks软件将均分球面所有有解的情况都找到了,分别如下:
- 当m=3,n=3,时,均分点的数量是4个,均分球面4个;
- 当m=3,n=4,时,均分点的数量是8个,均分球面6个;
- 当m=3,n=5,时,均分点的数量是20个,均分球面12个;
- 当m=4,n=3,时,均分点的数量是6个,均分球面8个;
- 当m=5,n=3,时,均分点的数量是12个,均分球面20个。
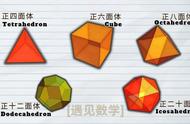
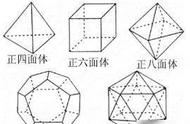
将球面上的均分点连接起来,就得到正多面体了,分别是正四面体,正六面体,正十二面 体,正八面体和正二十面体。
由以上证明或者验证可知,均分球面,只有5种情况有解,5种情况对应5种正多面体,因此正多面体只有5种。
本文主要让大家理解球面上均布孔和均分球面的概念,引起对正多面体感兴趣,为均分球面和正多面体的三维绘图,提供了一个设计思路。