双曲线渐近线方程和离心率的关系,则它的渐近线方程为

双曲线虽然没有椭圆和抛物线那样承担大梁，没有在解答题中出现。但是不代表高考不考，是选择题填空题的常客。双曲线不论怎么考，仅仅抓住定义、标准方程、渐近线、离心率，再结合一点平面几何的知识，完全能准确解答。

思考一：如图，利用OP是线段，OF₁的垂直平分线。可知∠F₁OP=∠POQ=∠QOF₂=60°，那么渐近线斜率可得，进而a，b关系可知再联想双曲线中a，b，c的关系，可得离心率e=2。

思考二：求出点Q的坐标，带入到渐近线方程。

关键是怎么求Q坐标，用两种方法来求：

1.因OP⊥F₁P，三角形F₁OP是直角三角形，tan∠F₁OP=b/a，又斜边是c，所以F₁P=b，OP=a.从而有P点坐标，P是F₁Q的中点，Q点坐标可求。把Q点带入渐近线方程，联系到双曲线中a，b，c的关系，可得离心率e=2。

2.可直接设Q(at,bt).t>0,利用向量Q F₁和向量Q F₂的数量积为0.求出t,Q点坐标就知。把Q点带入渐近线方程，联系到双曲线中a，b，c的关系，可得离心率e=2。

两种思路三种方法，哪种方法好，我认为适合自己，哪种更容易想到，哪种就是自己的好方法。对于离心率问题，往往就是找a和c的关系。因为教材有abc的一种平方关系了，所以再根据题目条件，任意两者之间找到一种关系即可。

2019年高考全国一卷理科16题：

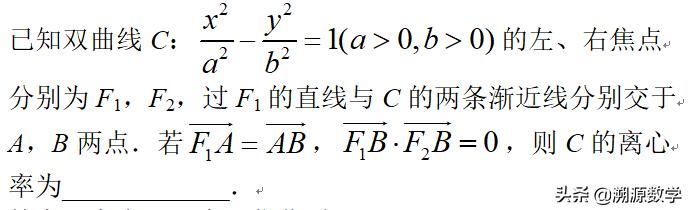
答案见留言区，亲，您作对了吗？