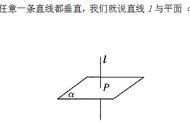
Φ是直线与平面的夹角，是90 - θ或θ的补角。我们知道cosθ= sin (90 - θ)所以Φ可以通过以下方式给出:
sinΦ=sin (90 – θ) = cos θ
举个例子更好理解这个问题：
空间的一条直线的方程是：
一个平面方程是：3x 4y – 12z = 7，求出它们的夹角。
解: 设θ是直线与平面法线的夹角。
因为直线过（0, -32, 2）这点， 而且其方向矢量为<6, 2, 3>
在矢量形式下，方程可以写成:
如何确定线面角的位置
阅读全文>>2023-05-25 16:41:38
线面成角标准步骤（线面成角怎么证明）
阅读全文>>2023-05-25 16:25:39
线面所成角图解（怎样找线与面所成角的大小）
阅读全文>>2023-05-25 16:37:24
线面角公式口诀（线面角求法公式）
阅读全文>>2023-05-25 16:36:06
线面角取值范围图解（求线面角图解）
阅读全文>>2023-05-25 16:54:10
线面角知识点（线面垂直知识点）
阅读全文>>2023-05-25 17:08:09
笔记本电脑无法开机（笔记本电脑无法开机什么原因）
阅读全文>>2023-05-25 16:29:31
笔记本激活windows（笔记本电脑激活windows）
阅读全文>>2023-05-25 16:26:20
最新win10永久激活方法（win10有没有永久激活的方法）
阅读全文>>2023-05-25 16:25:42
屠夫出装dota（屠夫出装攻略）
阅读全文>>2023-05-25 17:06:22
