答案是不可能，三根针永远不会互成120°。
当然了，前提是这个钟必须三根针每时每刻都在动，因为有些钟表是秒针绕一圈结束，分针才会动一格。
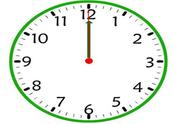
我们以钟表盘面建立极坐标，12点方向为正，顺时针角度为正。
（上图）为了方便，我们设三根指针长度都为1
秒针为OA，坐标为(1，α)
分钟为OB，坐标为（1，β）
时针为OC，坐标为(1，γ)
每个指针的角速度我们容易知道，因此每时每刻动了多少角度，我们就可以列出式子（下图）
如果时针转了6圈分针要转多少圈（时针转6圈分针转多少圈算式）
阅读全文>>2024-01-28 06:07:58
云端文件在哪里（云端保存的文件在哪）
阅读全文>>2024-01-28 06:17:06
云端怎么同步到本地（本地账户无法同步云端）
阅读全文>>2024-01-28 06:00:36
为什么同步不到云端（怎么知道自己手机开了同步云端）
阅读全文>>2024-01-28 06:26:55
手机云同步去哪里找（为什么手机经常云同步）
阅读全文>>2024-01-28 06:08:52
干物妹小埋为什么变小（干物妹小埋为何能变大变小）
阅读全文>>2024-01-28 06:31:32
干物妹小埋为何没有第三季（干物妹小埋真的没有第三季了吗）
阅读全文>>2024-01-28 06:06:53
为什么干物妹小埋回到家会变小（为啥干物妹小埋不出第三季）
阅读全文>>2024-01-28 06:14:46
干物妹小埋为什么不出第二季（干物妹小埋在日本有没有第三季）
阅读全文>>2024-01-28 06:35:11
