从逻辑的角度来对索引进行划分的话,可以分为单列索引、全文索引、组合索引和空间索引。其中单列索引又可分为主键索引、唯一索引和普通索引。这里的逻辑可以理解为从 SQL 语句的角度,或者是从数据库关系表的角度。下面就简单介绍这些索引的作用和用法,以及在修改表的时候如何添加索引。
主键索引
即主索引,根据主键建立索引,不允许重复,不允许空值;
主键:数据库表中一列或列组合(字段)的值,可唯一标识表中的每一行。
加速查询 列值唯一(不可以有) 表中只有一个
ALTER TABLE 'table_name' ADD PRIMARY KEY pk_index('col');
唯一索引
用来建立索引的列的值必须是唯一的,允许空值。唯一索引不允许表中任何两行具有相同的索引值。比方说,在 employee 表中职员的姓 name 上创建了唯一索引,那么就表示任何两个员工都不能同姓。
加速查询 列值唯一(可以有)
ALTER TABLE 'table_name' ADD UNIQUE index_name('col');
普通索引
用表中的普通列构建的索引,没有任何限制。
仅加速查询
ALTER TABLE 'table_name' ADD INDEX index_name('col');
全文索引
用大文本对象的列构建的索引
ALTER TABLE 'table_name' ADD FULLTEXT INDEX ft_index('col');
组合索引
用多个列组合构建的索引,这多个列中的值不允许有空值。
多列值组成一个索引,专门用于组合搜索,其效率大于索引合并。
ALTER TABLE 'table_name' ADD INDEX index_name('col1','col2','col3');
在对多列组合建立索引时,会遵循「最左前缀」原则。
最左前缀原则:顾名思义,就是最左优先,上例中我们创建了 (col1, col2, col3) 多列索引,相当于创建了 (col1) 单列索引,(col1, col2) 组合索引以及 (col1, col2, col3) 组合索引。
所以当我们在创建多列索引时,要根据业务场景,将 where 子句中使用最频繁的一列放在最左边。
空间索引
对空间数据类型的字段建立的索引,底层可通过 R 树实现。只不过使用较少,了解即可。

我们知道,索引的底层本身就是通过数据结构来进行实现的。那么根据其底层的结构,常见的索引类型可分为哈希索引,BTree 索引,B Tree 索引等。这里我们就主要来介绍这三种索引背后的实现机制。
哈希索引
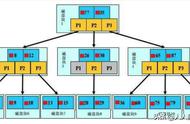
顾名思义,哈希索引是通过哈希表实现的。哈希表的特点在之前的文章「九大数据结构」中已经详细介绍过。通过哈希表的键值之间的对应关系,能够在查询时精确匹配索引的所有列。哈希索引将所有的根据索引列计算出来的哈希码存储在索引中,同时将指向每个数据行的指针保存在哈希表中。

上图是通过哈希索引查询行数据的示意图,可以发现哈希索引同样会发生哈希冲突,并且是通过链地址法解决冲突的。当发送冲突时,还需要对链表进行遍历对比,才能够找到最终的结果。
在 MySQL 中,只有 Memory 存储引擎显式的支持哈希索引,而innodb是隐式支持哈希索引的。
这里的隐式支持是指,innodb引擎有一个特殊的功能 “自适应哈希索引”,当innodb注意到一些索引值被使用的非常频繁时,且符合哈希特点(如每次查询的列都一样),它会在内存中基于 B-Tree 索引之上再创建一个哈希索引。这样就让 BTree 索引也具有哈希索引的一些有点。这是一个完全自动的、内部的行为。
由于哈希结构的特殊性,其用于非常高的检索效率,通过哈希函数的映射可以一步到位。但是同样也是因为结构的特殊,导致哈希索引只适用于某些特定的场合。哈希索引的限制[1]:
不支持范围查询,比如 WHERE a > 5;只支持等值比较查询,包括=、IN 、<=>
无法被用来避免数据的排序操作;因为经过了哈希函数的映射过程,使得丢失了哈希前后的大小关系,从而无法按照索引值的顺序存储。
不支持部分索引列的匹配查找,因为哈希索引始终使用索引列的全部内容来计算哈希值。例如在数据列 (A, B) 上建立哈希索引,如果查询只有数据列 A,则无法使用该索引。
无法避免表扫描。因为当出现哈希冲突的时候,存储引擎必须遍历链表(拉链法)中所有的行指针,逐行进行比较,直到找到所有符合条件的行。
哈希冲突很多的情况下,其索引维护的代价很高,并且性能并不一定会比 BTree 索引高。
BTree 索引
BTree 实际上是一颗多叉平衡搜索树。从名字可以看出,BTree 首先是一颗多叉搜索树,这意味着它是具有顺序的;其次 BTree 还是平衡的,这意味着它的左右子树高度差小于等于1。
事实上一颗 BTree 需要满足以下几个条件:
每个叶子结点的高度都是一样的;
每个非叶子结点由 n-1 个 key 和 n 个指针 point 组成,其中 d<=n<=2d, key 和 point 相互间隔,结点两端一定是 key;
叶子结点指针都为 ;
非叶子结点的key都是 [key, data] 二元组,其中 key 表示作为索引的键,data 为键值所在行的数据;
一颗常见的BTree树见下图。

这是一颗三阶的BTree,可通过键值的大小排序进行数据的查询和检索,其中叶子节点的指针都为空,因此省略没画。从上图可以发现,BTree 的树形状相较于我们之前常见的二叉树等结构,更为扁平和矮胖。
之所以这样设计,还是跟磁盘读取的特点有关。我们知道在建立索引时,也是需要占据物理空间的。而实际上当数据量比较大的时候,索引文件的大小也十分吓人。考虑到一个表上可能有多个索引、组合索引、数据行占用更小等情况,索引文件的大小可能达到物理盘中数据的1/10,甚至可达到1/3。
这就意味着索引无法全部装入内存之中。当通过索引对数据进行访问时,不可避免的需要对磁盘进行读写访问。同时我们还知道,内存的读写速度是磁盘的几个数量级。因此在对索引结构进行设计时要尽可能的减少对磁盘的读写次数,也就是所谓的磁盘 I/O 次数。
这也就是索引会采用 BTree 这种扁平树结构的原因,树的层数越少,磁盘I/O的次数自然就越少。不仅如此,我们上面提到过磁盘预读的局部性原理。根据这个原理再加上页表机制,能够在进行磁盘读取的时候更大化的提升性能。
BTree 相较于其它的二叉树结构,对磁盘的 I/O 次数已经非常少了。但是在实际的数据库应用中仍有些问题无法解决。
一是无法定位到数据行。通过 BTree 可以根据主键的排序定位出主键的位置,但是由于数据表的记录有多个字段,仅仅定位到主键是不够,还需要定位到数据行。虽然这个问题可以通过在 BTree 的节点中存储数据行或者增加定位的字段,但是这种方式会使得 BTree 的深度大幅度提高,从而也导致 I/O 次数的提高。
二是无法处理范围查询。在实际的应用中,数据库范围查询的频率非常高,而 BTree 只能定位到一个索引位置。虽然可以通过先后查询范围的左右界获得,但是这样的操作实际上无法很好的利用磁盘预读的局部性原理,先后查询可能会造成通过预读取的物理地址离散,使得 I/O 的效率并不高。
三是当数据量一大时,BTree的高度依旧会变得很高,搜索效率还是会大幅度的下降。
问题总是推动改进的前提。基于以上的问题考虑,就出现了对 BTree 的优化版本,也就是 B Tree。
B Tree索引
B Tree 一看就是在 BTree 的基础上做了改进,那么到底改变了什么呢。废话不多说,先上图。