一二年级,学生初步认识了长方形、正方形、平行四边形等平面图形的形状及特征,在后面的学习中还要进一步了解各图形的周长和面积,并用周长、面积公式解决实际问题。新课标要求,学习数学不仅要“知其然”还要“知其所以然”。因此,学生不仅要会用公式解决问题,还要知道这些公式是怎么推导出来的(以便日后忘记了公式也能自己“推”出来)。

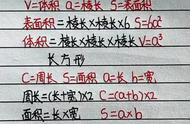
关于面积,在小学阶段需要掌握长方形、正方形、平行四边形、三角形、梯形、圆等6种平面图形的面积公式及应用。而长方形的面积公式是其他5种图形面积公式推导的基础,所以长方形面积公式的推理方法与其他5种图形的面积公式的推理方法也有所不同。长方形面积公式的推理方法用的是合情推理中的不完全归纳法,而正方形、平行四边形、三角形、梯形、圆等面积的推理方法则属于演绎推理中的三段论。下面进行具体分析:

“长方形、正方形面积的计算”是人教版数学三年级下册第60页的学习内容。教材首先呈现了两名学生用画格子或用面积单位测量长方形面积的活动,同时呈现了两种计数面积单位个数的方法,一种是1个1个地数数,这是最朴素、最基本的方法;另一种是数出每行的个数和行数,用乘法计算出面积单位的个数,为长方形面积公式的形成提供了直观经验。
例如“一个长方形长5厘米,宽3厘米。你能求出它的面积吗?”用画格子的方法把这个长方形分割成15个边长为1厘米的小正方形(长5厘米可以分成5段1厘米,宽3厘米可以分成3段1厘米,1个1个地数可以得到15个小方格),每个小正方形的面积是1平方厘米,那么15个小方格面积就是15平方厘米。还可以这样算:每行有5个小方格,共有3行,一共有几个小方格,也就是求3个5是多少,列出乘法算式为5×3(即长×宽)=15,得出15平方厘米。

因为一个例子还不能确定长方形的面积公式就是长×宽,所以教材安排了用1平方厘米的正方形拼摆多个长方形的活动,并用表格记录长、宽和面积。旨在通过数据,发现正方形的个数与长、宽之间的关系,即正方形的个数=长×宽,并且正方形的个数有几个,长方形的面积就是几平方厘米。由此可以概括出“长方形的面积=长×宽”。这种通过观察多组正方形拼摆长方形的数据,发现它们都有“正方形的个数=长×宽”这种相同的性质,推出“长方形的面积=长×宽”的一般性结论的推理方法就是不完全归纳法。