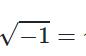虚数和复数是数学中的概念,用于描述在实数范围之外的数。
虚数是一个实部为零的复数,用一个非零实数乘以虚数单位 i(满足 i²=-1)表示。例如,2i 是一个虚数,因为它的实部为零。虚数在数学和物理学中有广泛的应用,如在电路分析、量子力学、信号处理等领域中。
复数是一个有实部和虚部的数,通常表示为 a bi 的形式,其中 a 和 b 是实数,i 是虚数单位。实部是复数的实数部分,虚部是复数的虚数部分。例如,3 4i 是一个复数,其中实部为 3,虚部为 4。复数在代数、几何、物理学、工程学等领域中都有广泛的应用,如在复分析、复变函数、矩阵分析、量子力学等领域中。
二、虚数什么时候发明的,有哪些有意思的故事虚数的概念最早可以追溯到16世纪意大利数学家Gerolamo Cardano,但是在当时并没有得到广泛的认可和使用。虚数的概念真正被广泛应用是在18世纪后期和19世纪初期。
以下是一些关于虚数的有趣故事:
- 历史上,虚数经常被认为是荒谬、无用的概念。16世纪时,Gerolamo Cardano曾经将其描述为“绝对不可能的数”,并将其称为“虚数”。直到18世纪后期,欧拉和其他数学家才开始使用虚数,并在数学中得到广泛应用。
- 在19世纪初期,德国数学家卡尔·弗里德里希·高斯发现了复数的代数和几何性质,并发明了复数平面。这是一个将复数表示为平面上的点的图形表示方法,使得复数的运算和性质更加直观。
- 在19世纪中叶,英国数学家威廉·汉密尔顿致力于寻找一个类似于实数轴的结构来表示复数。在一次散步中,他突然想到可以用三元组(a, b, c)表示复数 a bi cj,其中 i²=j²=-1,ij=-ji。这种三元组被称为四元数,它不仅可以表示复数,还可以表示向量和旋转等概念。
- 在20世纪,数学家们继续推广虚数和复数的概念,并发现了更多有趣的性质。例如,复数可以用极坐标表示,虚数可以用指数函数表示。虚数和复数在物理学、工程学、计算机科学等领域中有广泛的应用,如在电路分析、量子力学、信号处理、图像处理、密码学等领域中。
复数的概念起源可以追溯到16世纪意大利数学家Girolamo Cardano,但直到18世纪后期和19世纪初期才被广泛认可和应用。
以下是一些关于复数的有趣故事:
- 在16世纪,意大利数学家Girolamo Cardano研究方程时遇到了负数的平方根,他称其为“fictae radices”,也就是虚数的意思。但当时虚数并没有得到广泛的认可和使用。
- 在18世纪后期,瑞士数学家欧拉(Euler)开始使用复数,并发现了它们的代数和几何性质。欧拉发现了著名的欧拉公式 e^(iπ) 1 = 0,这个公式将五个最基本的数学常数(0、1、e、i和π)连接在了一起,被誉为数学中最美丽的公式之一。
- 在19世纪初期,德国数学家高斯(Gauss)发现了复数的性质和运算法则,他把复数看作是实数的自然推广。高斯发明了复数平面,把复数表示成平面上的点,这个表示法直观地展示了复数的代数和几何性质。
- 在19世纪中叶,爱尔兰数学家威廉·罗兰·哈密顿(William Rowan Hamilton)致力于寻找一种结构来表示复数,他在一次散步中突然想到可以用三元组 (a, b, c) 表示复数 a bi cj,其中 i²=j²=-1,ij=-ji。这种三元组被称为四元数,它不仅可以表示复数,还可以表示向量和旋转等概念。
- 在20世纪,数学家们继续推广复数的概念,并发现了更多有趣的性质。例如,复数可以用极坐标表示,虚数可以用指数函数表示。复数在物理学、工程学、计算机科学等领域中有广泛的应用,如在电路分析、量子力学、信号处理、图像处理、密码学等领域中。