上一夜我们谈到了双曲线的离心率,无独有偶,今晚我们继续探讨椭圆的离心率。如果愿意,关于离心率的问题,我们至少可以玩上一年。

好了,直接上题。

初次见到此题,我知道你的内心几乎是崩溃的。你甚至连什么是内心,什么是重心都没有搞清楚,还求个什么离心率。
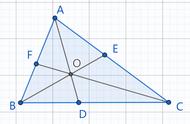
内心即三角形内切圆的圆心,角平分线的交点,重心则是三角形中线的交点。以三角形的四心问题作为背景,是常考的模式。如果说本题很难,一定不是题目本身的问题,而是你欠缺一些常用的二级结论。比如本题中的平行、三角形的面积、椭圆的焦点三角形等等。
首先,设出重心坐标与内切圆的半径,通过平行建立重心坐标与半径的关系;然后,通过等面积法得出基本量的关系,进而得出离心率。
从步骤上来说,是不是很简单?
是,站着说话不腰疼。

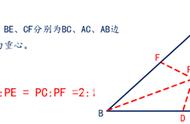
角平分线定理结合等比的性质,求得内心分非焦点角平分线的比值与离心率的关系;然后借助相似三角形求得比值,进而求出离心率。
坦白说,我十分欣赏法2这种巧妙而不不露声色的绝*,看似高深莫测,实则大道至简。值得一提的是,法2中的内心与离心率的关系可以作为结论的。
夜,那么长,以数学疗人寂寞,不是修行,就是罪过。
叨叨
2019.4.16
,