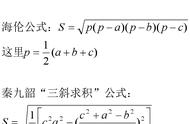从简洁易算来说,海伦的写法更胜一筹。
那海伦是谁呢?
提到海伦,再加一个词古希腊,让我想到的是一个倾国倾城的大美女——特洛伊战争里的世界上最漂亮的女性,海伦。这是一个希腊神话故事,我只记得金苹果,希腊众神,特洛伊长达10年的战争,《荷马史诗》里描述海伦的美貌并没有正面描述,而是侧面描写,当战争进行到第九年时,希腊联军兵临城下,特洛伊危在旦夕,特洛伊的长老们坐在城楼上,海伦来到城楼上,他们说出了为这样的美女打这么一场战争,并不后悔。
可惜今天要说的海伦,不是一个美女,甚至不是一个女性,而是一个男性,网上的配图是个大络腮胡的男人。
海伦生平未知,推测是希腊公元62年左右生活的人,大概在亚历山大城教过数学和物理等课程,是古希腊数学家,力学家和机械学家。
他编著的有《度量论》,《武器制造法》,《测量仪器》,《气体力学》,《自动机建造技术》,《定义》,《几何》《测量》《测体积学》等。神奇的是竟然都没有失传。
《度量论》本来以为遗失了,但是1896年德国人舍内(R.Schone)在君士坦丁堡发现了他编著的《度量论》一本手抄本,于1903年由其子H·舍内校订出版,其中海伦公式的证明就记录于此书第二卷。
其实历史学家推论海伦的生活时代也很有意思,大家可以百度看看,比如通过某个著作,得出他生活在某个时代之前,通过某个著作得出他生活在某个时代之后,最后根据他著作里的月食得出他必定生活在公元62年左右,因为月食的时间是可以推算并且固定的。如果没记错历史上很多模糊的时间,都可以通过文献记录当时的日月食推算出具体时间。有时候时间就是这么奇妙。
海伦公式的在四边形的推广
当我们发现三角形的海伦公式后,就会有人想把它推广到四边形,五边形,六边形……甚至n边形。
然而,我们都知道四边形是不稳定的,甚至五边形,六边形……n边形都是不稳定的。
我们一般计算某四边形的面积,就必须添加其他的限定条件,比如角或者对角线等等。
波罗摩及多(公元598-660)就给出一个圆内接四边形的面积公式,四边长分别是a,b,c,d,p=(a b c d)/2

在对于一般的四边形,依然有面积公式:

A B为四边形对角和,同样C D也为另一对对角和。
那么圆内接四边形的对角和的一半就等于90度,余弦为0。
说一下:我百科了一个公式出来,当时有一点疑惑这个公式
既然是对角和一半,后来公式里又有2倍,那为什么不直接用对角和呢?然后带着疑问就查查资料,自己证明下,发现百科的公式是错误的。