(bluehouse456 全文整理)
很高兴能和大家一起学数学。
今天我们的学习内容是人教版五年级上册小数除法单元中上的近似数。
在上一单元。
我们学习小数乘法时,曾学过求积的近似数。
咱们先来复习怎样求积的近似数吧。
还记得是用什么方法吗?
请你根据给出的乘法竖式。
把结果保留相应的小数位数。
小童说。
我记得是用四舍五入的方法求积的近似数。
结果保留一位小数。
就看小数部分第二位。
四小于五可以舍去。
最后约等于2.5。
小瑞说。
如果要保留两位小数。
我们就看小数部分第三位。
七大于五,向前一位进一。
结果约等于2.55。
看来你们已经掌握了求积的近似数的方法。
接下来我们要学习小数除法中商的近似数。
你们有什么想法吗?
我觉得小数除法中也应该会求商的近似数,我想知道什么时候需要求商的近似数?
如果需要,求商的近似数。
方法和求积的近似数一样吗?
同学们特别善于思考。
能够通过求积的近似数联想到求商的近似数。
那么今天这节课,我们就一起来研究研究你们的问题吧。
羽毛球是一项老少皆宜的运动,可以强身健体。
深受人们的喜爱。
王鹏最近就喜欢上了这项运动。
作为初学者,爸爸给他买了一桶羽毛球。
我们一起来看看。
观察这幅图。
从中你能得到什么信息?
能提出什么数学问题吗?
小丁说。
我知道了,一桶羽毛球有12个。
总价是19.86元。
所以我就想问。
每个羽毛球大约多少钱?
怎么样?
小丁提出的问题,你们有想法吗?
可以写一写,算一算,求出每个羽毛球大约多少钱?
把你解决问题的过程记录下来。
开始吧。
你们看。
老师,这里收集了两个同学的作品。
仔细观察他们的做法。
有什么相同,有什么不同?
小瑞说。
它们竖式的商是一样的。
但横式的结果,小东是用精确值表示。
小芳却求了商的近似数。
是呀。
小芳,为什么要求商的近似数呢?
让我们听听小芳是怎么说的吧,因为这道题是求每个羽毛球多少钱。在学习鸡的金丝数时,我们知道人民币的最小面值是分。
如果乘积的小数位数比较多,应该保留两位小数,精确到分,我看计算出的商是三位小数,就把结果保留了两位小数,这样比较符合实际情况。
原来,小芳是借助求积的近似数时计算价钱的经验,联想到要求羽毛球的单价也应该根据人民币面值的特点,把结果保留两位小数,求商的近似数。
怎么样,你们听明白了吗?
再来具体说说怎样把求出的商保留两位小数。
我用的是四舍五入的方法,保留两位小数,所以要看小数部分第三位上的数,如果大于等于五,就向前一位进一,如果小于五,就舍这道题。商的小数部分第三位是五,所以应该向前一位进一,最后结果约等于1.66元。
那如果要求保留一位小数精确到角呢?
如果保留一位小数,就看小数部分第二位上的数是五,按四舍五入的方法,结果约等于1.7元。
现在每个羽毛球价格的问题我们已经解决了。
大家还记得刚上课时文文提出的问题吗?
在用小数除法解决问题时,什么时候需要求商的近似数?
通过上面问题的解决,相信你们已经找到了答案。
其实,在实际应用中,小数除法所得的商也可以根据需要按四舍五入法保留一定的小数位数,求出商的近似数。
经过一段时间的练习,王鹏已经跻身羽毛球运动发烧友的行列。
一次,他在逛体育用品超市的时候,发现了爸爸送他的同款羽毛球有优惠活动。
每桶有12个,售价18.5元。
你们猜猜王鹏看到这个信息会想什么?
小韩说。
我猜他一定想知道平均每个羽毛球大约多少钱。
那咱们就算算在这家超市每个羽毛球大约多少钱?
得数保留两位小数。
把你解决问题的过程记录下来,开始吧。
我发现有的同学已经算完了。
有的同学还在继续算。
然而,有的同学却皱起了眉头。
那我们来看看大家都遇到了什么样的问题。
小明说。
我发现这道题怎么算都除不尽。
都算了半天了,还没算完?
同学们。
小明说的,你发现了吗?
是不是也遇到了同样的困难?
面对这种情况,你们有什么想法?
小瑞说。
必须算完才能求商的近似数吗?
那我们带着小明和小瑞的问题,看看其他同学都是怎么做的吧。
仔细观察这两位同学的做法。
有什么相同,有什么不同?
我发现他们的答案都是1.54元,但是竖式有点不太一样,小彤算到了小数部分第四位,而小亮只算到了小数部分第三位。
我觉得小童往下多商一位也可以,但是没有必要,因为题目要求保留两位小数,所以只需要把商的小数部分第三位算出来,在四舍五入就可以了,就像小亮一样,已经算出来商的小数部分第三位是一,直接舍去就行,没有必要接着往下除了。
我明白了,在四舍五入的时候,看的是要保留的下一位是几?这道题要保留两位小数,我们只要计算到小数部分第三位,就能求近似数了,除不尽也没关系。
现在,我们一起将横式的结果补充完整。
老师,还想问问大家,如果这道题不是有关价钱的实际问题。
只是一道除法计算题。
要求把结果保留三位小数,你又会怎么做呢?
小林说,我会计算到小数部分第四位,然后四舍五入。
这道题第四位,商六。
根据四舍五入的原则,最后结果约等于1.542。
小韩说。
以此类推,如果要求保留四位小数,我会计算到小数部分第五位。
再把第五位四舍五入。
结果约等于1.5417。
现在我们就结合刚才小林和小韩的发言,说一说怎样求商的近似数。
小丁总结道。
我们在求商的近似数时。
计算到比要保留的小数位数多一位。
再将最后一位四舍五入就可以了。
其实在解决这个问题时,老师发现还有同学是这样做的。
你们来看一看,有没有什么疑问?
他都没有计算到小数部分第三位,怎么就求近似数了,这样做行吗?
是呀,没计算到第三位,就把第三位上的数舍去,这样做能行吗?
你们是不是也和小兰有同样的疑问?
小勇是怎么想的?
让我们听听他的想法吧。
因为我算到小数部分第二位之后,发现余数是二二,如果添零继续除,最多也就商11比5小,所以我就不除了,直接按照四舍的方法求出近似数。
哦,我明白了,虽然小勇没有算出商的小数部分的第三位,但是通过余数估出第三位肯定比五小,也能求出近似数,所以他这样做也是对的。
我觉得他们说的有道理,如果估出下一位的商等于或大于五,就可以按照向前一位进一的方法来求商的近似数。
要是比武小,就舍弃。
虽然小勇只除到了小数部分,第二位没有继续往下出,但是只要估出下一位的商是几?
就可以用四舍五入的方法来求近似数。
同学们太棒了,找到了利用估算来解决问题的途径。
虽然方法不尽相同,却能得到相同的答案。
同学们,咱们在帮王鹏解决买羽毛球问题的过程中,学会了求商的近似数。
这是小亮刚上课时提出的问题,他是这样问的。
求商的近似数和求积的近似数方法一样吗?
说说吧,现在你知道它们之间有什么区别和联系了吗?
文文说,无论是求商的近似数,还是求积的近似数。
都要根据实际情况或者题目要求保留相应的小数位数,然后求近似数。
小明补充说。
而且在求近似数时,都是用四舍五入的方法。
小勇说。
不同点是,求商的近似数时不用算完,只要计算到比要保留的小数位数多一位就行了。
而求积的近似数时,要计算出乘积后再求近似数。
学会了求商的近似数,相信你们一定能解决下面的问题。
请根据给出的除法竖式,按要求求出商的近似数。
再具体说说你是怎样求的近似数?
小兰说。
保留一位小数,看小数部分,第二位是九。
应该向前一位进一。
最后结果约等于0.4。
文文说。
保留两位小数,看小数部分,第三位是七。
所以应该向前一位进一。
最后结果约等于0.40。
这时,小静提出了他的疑问。
保留一位小数,最后的结果是0.4。
保留两位小数,最后的结果是0.40。
有什么区别吗?
小芳回答道。
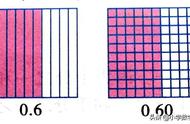
0.4表示精确到十分位。
而0.40表示精确到百分位。
所以在表示近似数时,小数末尾的零不能划掉。
真好。
咱们再来看第三小题。
保留三位小数,你们是怎么解决的?
我的方法是在余数十七后面添零,继续除,算出第四位商四,余十四四小于五要舍去,结果约等于0.397。
我发现余数是17,如果添零继续除,可以把除数39估成40,估出下一位的商是小于五的,可以直接舍弃,所以保留三位小数,结果约等于0.397。
这两种方法都是可行的。
只要我们能够知道被保留位数的下一位的商是大于等于五还是小于五,就能按照要求求出商的近似数。
接下来这个任务,需要你们结合实际情况,选择合适的方法来解决问题。
看看你能从题目中了解到哪些信息。
小勇说,我知道了,铺路队上午工作3.5小时,铺路164.9米。
下午工作4.5小时,铺路206.7米。
要解决的问题是上午铺路速度快,还是下午速度快?
请你写一写,算一算。
选择合适的方法解决问题。
把过程记录下来。
开始吧。
屏幕前的同学们,你们都完成了吗?
我们先来看看小明是怎样做的。
我先算出上午的速度,用164.9除以3.5竖式,我先算到了小数部分第一位。
得47.1没继续往下算,想先看看下午的速度大概是多少。
用206.7除以4.5同样算到小数部分第一位,发现得数是45.9。
很明显,保留整数就可以比较出大小了。上午47.1保留整数约等于47米,下午45.9,保留整数约等于46米。因为47大于46,所以上午铺路的速度快。
你们听明白了吗?为什么小明只保留整数,而不再继续往下除了呢?
小东说,因为上午的速度保留整数,即使舍去十分位上的数,还得47米每小时。
而下午的速度,哪怕把十分位上的数向前一位进一,也才只有46米每小时。
很显然,保留整数就能知道山五铺路的速度更快。
看来,我们在解决问题时,要根据实际需要求商的近似数。
可是万一我们四舍五入后的结果是一样的,又该怎么办呢?
留给大家课后去思考。
同学们,通过这节课的学习,你们都有哪些收获?
我学会了求商的近似数的方法,在求商的近似数时,计算到比要保留的小数位数多一位,再将最后一位四舍五入。
我们从求积的近似数联想到求商的近似数,说明知识之间是有联系的。
我知道了,在解决问题时需要根据实际情况求近似数。
确实,数学和生活是密不可分的,解决问题的方法也是多样的。
今天,同学们通过知识间的联系,从积的近似数联想到商的近似数,进而提出了想要研究的问题,又在探究问题和解决问题的过程中学会了新的知识。
今天我们学习的内容在数学书第32页,大家课后可以自主复习圈画重点。
课后练习一、完成数学书第36页第一题中圈出的题目。
二完成数学书第37页第八题。
同学们,这节课我们就上到这里,再见。
,