如果一个两位数的个位数字是a,十位数字是b,那么如何表示出这两个数呢?是不是直接写ab呢?要知道如何表示这个两位数,我们需要理解数位上的数字和数位之间的关系,从而能够正确地表示出一个数。本篇文章,我们主要介绍以下几个方面的内容,(1)数的表示;(2)倍数关系;(3)阅读理解型;(4)“魔术”题(数字游戏)。

个位上的计数单位为“个(一)”,比如个位上的数字为a,那么表示有a个一,即a;十位上的计数单位为“十”,比如十位上的数字为b,那么表示有b个十,即10b;百位上的计算单位为“百”,比如百位上的数字为c,那么表示有c个百,即100c,那么这个三位数为:100c 10b a。
1.用代数式表示数例题1:一个两位数的个位数字是a,十位数字比个位数字的2倍少1,用含a的代数式表示这个两位数。
分析:个数数字为a,十位数字比个位数字的2倍少1,那么十位上的数字为2a-1,表示用10个2a-1,即为10(2a-1),即可表示出该两位数。这个两位数可以表示为:10(2a-1) a=20a-10 a=21a-10,表示好后记得化简。

例题2:一个两位数,个位数字是a,十位数字是b,交换个位数字和十位数字的位置得到一个新的两位数,这两个两位数的差是否能被9整除?
分析:分别表示出原两位数和新两位数,做差进行探索倍数关系。
(10b a)-(10a b)=10b a-10a-b=9b-9a=9(b-a),
∴这两个两位数的差能被9整除.
本题还涉及一个小知识点,整除问题。如果要证明能被某个数整除,那么我们需要将其表示为这个数倍数的形式。比如能被3整除,那么表示为3a的形式;能被9整除,那么表示为9a的形式;能被11整除,那么表示为11a的形式等等(注:a可以是单独的字母,也可以是代数式)。
变式1:这两个两位数的和是否能被11整除?
分析:考查方式与例题2一样,还是分别表示出两个数,然后求和,再探索倍数关系。(10b a) (10a b)=10b a 10a b=11b 11a=11(b a),
∴这两个两位数的和能被11整除.
变式2:若新的两位数大于原来的两位数,求a与b的大小关系。
分析:10a b>10b a,∴10a-a>10b-b,∴9a>9b,∴a>b.

例题3:定义:对任意一个两位数a,如果a满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“迥异数”.将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如:a=12,对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为21 12=33,和与11的商为33÷11=3,所以f(12)=3.如果一个“迥异数”b的十位数字是k,个位数字是2(k 1),且f(b)=11,请求出“迥异数”b.
分析:阅读理解型问题的解题关键是读懂题意,本题涉及两个概念:(1)迥异数,这个应该比较容易,满足两个条件即可,供我们在解题时得到答案后验证使用;(2)f(a),指的是把这个新两位数与原两位数的和与11的商。
理解这两个概念后,我们需要先表示出新两位数与原两位数的和。
即:12k 2 21k 20=33k 22,那么f(b)=(33k 22)÷11=3k 2
又因为f(b)=11,那么3k 2=11,可得到k的值为3,所以b=10×3 2×(3 1)=38。

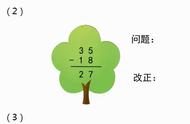
例题4:小刚对小强说:你任意写一个两位数,满足十位数字比个位数字大2;然后交换十位数字与个位数字,得到一个新的两位数;最后用其中较大的两位数减去较小的两位数.我就能知道这个差是多少.你知道这是为什么吗?这个差是多少呢?
解:设原来的十位数,十位数字为x,则个位数字为:(x-2),
故两位数是:10x x-2=11x-2,
交换十位数字与个位数字,得到的十位数是:10(x-2) x=11x-20,
故11x-2-(11x-20)=18,
即较大的两位数减去较小的两位数的差为18.
,