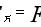哈喽,大家好!
在前面的文章我们探索了关于行星运动规律的二级结论,从整个行星围绕中心天体运动的尺度看清了运动基本规律以及中心天体与这种运动之间的代数联系。今天让我们把视角移到中心天体,从自转的角度探索单个星体尺度上的一些二级结论与公式。
友情提示:今天这些二级公式对 自转 、黑洞 相关的题目帮助尤其的大。由于黑洞方面的题目所涉及的知识不会太深,自转的题目也相对比较固定,因此在这节内容上,二级公式可以说是做选择题的不二法宝。
废话不多说,上菜!
【黑洞】
黑洞在教材上只是简短的说明,有兴趣的同学可以了解一下更多的知识:

黑洞
黑洞(英文:Black Hole)是现代广义相对论中,存在于宇宙空间中的一种天体。黑洞的引力极其强大,使得视界内的逃逸速度大于光速。故而,“黑洞是时空曲率大到光都无法从其事件视界逃脱的天体”。
当然,我们做题不需要了解这么深,仅需知道黑洞最基本的定义即可:
一个逃逸速度大于等于光速的天体就叫它黑洞。
因此,看一个天体会不会成为黑洞、能不能成为黑洞、什么时候成为黑洞,只有一个标准,就看它的逃逸速度有多大。
那逃逸速度怎么算呢?
它是物质无动力脱离引力束缚所需的最小速度,是第一宇宙速度的√2倍。
至于为什么是√2倍,可用大学物理轻松证明,这里不做过多阐述,不过它非常重要,对所有星体都适用。
为方便研究,我们规定一下:天体质量为M,半径为R,万有引力常量为G,重力加速度为g
第一宇宙速度我们都清楚怎么算,我们令第一宇宙速度为 v1 ,第二宇宙速度(逃逸速度)为 v2,则有 :

第一、第二宇宙速度
令 v2= c(光速),再利用黄金代换将g消掉,我们不难得出:

施瓦西半径公式
Rs为施瓦西半径,小于这个临界值便会演绎成黑洞。
其实做题时半径本身并不重要,重要的是M与R的比值,才真正决定要不要成为黑洞: