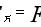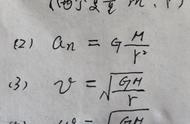【万有引力的复习】总则
(一)基本规律
一、开普勒行星运动定律
1.椭圆轨道定律:所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
2.等面积定律:对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积。
3.恒比值定律:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。
二、万有引力定律
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与两物体的质量Mm的乘积成正比,与它们之间距离r的二次方成反比。
2.表达式:F=GMm/r2(是r的平方,排版中上标打不出来),G为引力常量,其值为G=6.67×10-11 N·m2/kg2,(10的负11次方))。
引力常量是卡文迪许通过扭秤实验得出的。扭秤实验中用到了镜尺放大法、力矩平衡放大法。
3.万有引力公式适用条件
(1)公式适用于质点间的相互作用。当两个物体间的距离远远大于物体本身的大小时,物体可视为质点。
(2)天体之间。距离就是两天体球心之间的距离。
(二)应用
一、对天体质量和密度的计算
1.“黄金代换法”法(g-R)
利用天体表面的重力加速度g和天体半径R之间的关系,由某物的重力等于它收到的万有引力可得到GM=gR2称为黄金代换公式。拓展
GM=g'(R h)2。h为离星球表面的高度。
这样可以得到M的表达式,再利用密度公式ρ=M/(4πR3/3),就可以求某天体的密度。
2.“借助外援”法(T-r)
测出卫星绕天体做匀速圆周运动的周期T和半径r。
(1)由卫星受到的万有引力等于它圆周运动的向心力,就可得天体的质量M=____。
(2)若已知天体的半径R,就继续可求天体的密度ρ。
(3)若卫星绕天体表面运行时,如果贴着表面运动是,我们往往认为轨道半径r等于天体半径R。
可见,只要测出卫星环绕天体表面运动的周期T,就可估算出中心天体的密度。
二、非质点类的万有引力计算
公式适用于质点、均匀介质球体或球壳之间万有引力的计算。当两物体为匀质球体或球壳时,可以认为匀质球体或球壳的质量集中于球心,r为两球心的距离,引力的方向沿两球心的连线。
1若质点在匀质球壳的空腔内任意位置处,质点受到球壳的万有引力的合力为零,即∑F=0。
2在匀质球体内部距离球心r处的质点(m)受到的万有引力等于球体内半径为r的同心球体(M′)对它的引力
3.填补法求解万有引力
运用“填补法”解题的关键是紧扣万有引力定律的适用条件,先填补后运算,运用“填补法”解题主要体现了等效思想。
4.微元累积法
把施力物体分成无穷多个质点,先分析一个质点对物体的作用力,然后再矢量累积求。
三、天体类运动
先画出旋转模型 不论是求旋转天体还是中心天体的物理量,记住,都是以旋转天体为研究对象列方程。方程等式的左边是该处旋转天体受到的万有引力或者重力,等式的右边是向心力公式。这样就可以求解。
注意三类,在地随地球旋转,贴地飞行,离地飞行,三种情况的不同。在地问题是万有引力与重力的差异充当向心力;贴地,是地表处物体受到的重力或者万有引力全部充当向心力(忽略地球自转就等于忽略此处重力与万有引力的差异);离地,是该处物体受到的重力或者万有引力全部充当向心力(不考虑地球自转了,也就等于认为此处物体的重力与万有引力相等了)。
四、双星运动三大特点。
1.双星各自圆周运动的向心力是各自受到的万有引力,是相等的。
2.周期一样,即角速度相同
3.双星各自旋转的半径与质量成反比。
,