乔治布尔
布尔代数是基于二进制逻辑,其中只有两个可能的值:真(表示为1)和假(表示为0)。布尔代数主要关注三个基本运算:与(用符号∧表示,表示两个命题同时为真时结果为真,否则为假)、或(用符号∨表示,表示两个命题中至少一个为真时结果为真,否则为假)和非(用符号¬表示,表示取反操作,即真变为假,假变为真)。
布尔代数的应用非常广泛。它可以用于开关电路的设计和分析,布尔代数的运算可以表示电路的逻辑功能。此外,布尔代数还可以应用于计算机科学中的逻辑设计、编程和算法分析。逻辑运算在程序中广泛使用,布尔代数为程序员提供了一种简洁和有效的方式来处理逻辑问题。
乔治·布尔的布尔代数对现代计算机科学和逻辑推理有重要的影响。它为我们提供了一种系统化和严谨的方法来处理逻辑问题,为计算机系统的设计和开发提供了理论基础。布尔代数在逻辑学、电子工程和计算机科学等领域发挥着重要的作用,并成为现代信息社会中不可或缺的基础。
给出乔治布尔的布尔代数把逻辑学中的形式逻辑 的判断转化数学中的布尔代数的计算的伟大价值与意义
乔治·布尔的布尔代数的伟大价值和意义在于将逻辑学中的形式逻辑转化为了数学中的布尔代数,从而通过符号和运算规则的严谨性,使得逻辑推理可以更加精确和系统化。以下是它的几个具体的价值和意义:
- 精确且系统化的表达:布尔代数提供了一种精确的语言和符号系统,让我们能够准确地表示和符号化逻辑判断。通过使用逻辑运算符号和规则,逻辑推理可以被转化为一系列符号操作,增加了推理的清晰度和准确性。这种精确和系统化的表达为逻辑学的发展奠定了基础。
- 简化推理和分析过程:布尔代数的运算规则使得逻辑推理和分析的过程可以通过代数计算来完成。通过将逻辑判断和关系转化为布尔表达式,并应用布尔代数运算,我们可以进行逻辑判断的简化、化简和等价变形。这种代数计算的方法不仅使得推理过程更加简化和系统化,还提供了一种验证推理正确性的可靠方法。
- 应用于电路设计和计算机科学:布尔代数为电路设计和计算机科学领域提供了重要的理论基础。布尔代数中的逻辑运算与门电路的逻辑运算对应,这使得我们能够使用布尔代数来设计、分析和优化数字电路。此外,计算机科学中的编程语言和算法设计也广泛使用了布尔代数的概念和运算规则,例如逻辑表达式、条件语句和逻辑运算符号的应用。
- 推动了数理逻辑和计算机科学的发展:布尔代数为数理逻辑和计算机科学提供了数学化的框架和工具,推动了这些领域的发展。它为逻辑学的形式化提供了基础,将逻辑问题转化为了一种可以计算和证明的形式系统。同时,布尔代数在计算机科学中的应用推动了计算机技术的快速发展和进步,为现代计算机系统的设计和优化奠定了基础。
综上所述,乔治·布尔的布尔代数的伟大价值和意义在于将逻辑学中的形式逻辑转化为了数学中的布尔代数,从而为逻辑推理提供了精确、系统化和可计算的方法。它不仅简化了逻辑推理和分析过程,而且为电路设计和计算机科学建立了一种理论基础,推动了数理逻辑和计算机科学的发展。布尔代数成为了现代信息社会中不可或缺的基础,并对我们的日常生活和科技进步产生了巨大的影响。
你知道克劳德香农的硕士论文吗?
克劳德·香农(Claude Shannon)的硕士论文。他的硕士论文题目是《符号逻辑中的符号演算》(Symbolic Analysis of Switching and Relay Circuits),于1937年发表。

克劳德香农
这篇论文是香农在麻省理工学院完成的,它被视为现代数字电子和计算机科学的基石之一。在这篇论文中,香农提出了两个重要的概念:布尔代数和开关代数。他利用布尔代数来描述逻辑门的运行原理,并使用开关代数来分析电路的开关行为。
这篇论文的贡献之一是将布尔代数的原理应用于电路设计中,从而使得数字电子电路的设计和分析更加系统化和可靠。此外,香农还引入了离散数学的思想,将电路中的开关抽象为逻辑门和符号。这种抽象和符号演算的方法为计算机科学奠定了基础。
总的来说,克劳德·香农的硕士论文具有里程碑意义,对数字电子和计算机科学的发展产生了深远影响,对现代信息理论和通信技术的发展也有着重要贡献。
克劳德香农的硕士论文《符号逻辑中的符号演算》的主要内容与观点,至少600字
克劳德·香农的硕士论文《符号逻辑中的符号演算》(Symbolic Analysis of Switching and Relay Circuits)于1937年发表,该论文被认为是现代数字电子和计算机科学的重要里程碑之一。香农在这篇论文中提出了许多重要的概念和观点,以下将详细介绍。
首先,香农引入了布尔代数的概念。他发现,布尔代数能够用逻辑运算和真值表来描述和分析逻辑函数的运算规则。通过将逻辑运算符(如与、或、非)与布尔变量和真值表相结合,香农构建了一种分析和设计数字电路的方法。这种方法可以将电路中的开关表示为逻辑门,使得电路设计变得更加系统化和可行。
其次,香农提出了开关代数的概念。他将开关抽象为具有两种状态(开和关)的符号,并使用开关代数来分析电路的开关行为。通过使用开关代数,香农能够推导出电路中各个开关元件之间的关系,并通过逻辑运算来模拟和分析电路的行为。这种开关代数的方法不仅简化了电路分析的过程,而且为电路设计提供了一种全新的思路。
第三,论文中还介绍了一种将电路中的开关行为和逻辑函数之间进行转换的方法。香农认为,每个逻辑函数都可以用一套等效的开关电路来表示,而每个开关电路也可以用一个逻辑函数来描述。通过这种等效转换,香农为电路设计者提供了一种灵活的设计方法,可以根据问题的需要选择合适的表达方式。
论文中的另一个重要观点是,香农强调了离散数学在电路设计中的重要性。他认为,使用离散数学的思维方式可以更好地抽象和描述开关电路的行为。通过将电路中的信号和状态抽象为离散的数学对象,香农开启了将离散数学应用于电子工程的新领域。
最后,香农还在论文中提出了一种二进制码的编码方法,这种方法被广泛应用于数字电路中的数据传输和错误检测。他通过使用二进制码来表示和传输信息,提出了一种更高效和可靠的数据传输方法,为后来的通信技术和信息理论的发展奠定了基础。
总结起来,克劳德·香农的硕士论文《符号逻辑中的符号演算》在数字电子和计算机科学领域引入了许多重要的观点和方法。他的研究不仅推动了电路设计的发展,而且对信息理论和通信技术的发展产生了深远影响。此外,香农的论文还强调了离散数学的重要性,为电子工程师和计算机科学家们提供了新的思维方式和解决问题的方法。
你知道冯诺依曼结构体系吗?
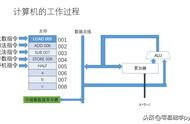
冯·诺依曼结构体系是计算机结构的一种基本设计原则,由匈牙利数学家冯·诺依曼在20世纪40年代提出。该结构体系将计算机分为五个主要组成部分:输入设备、输出设备、存储器、控制单元和算术逻辑单元(ALU)。
在冯·诺依曼结构体系中,指令和数据都以二进制形式存储在存储器中,并通过数据总线进行传递。控制单元负责解释和执行存储器中的指令,控制数据的传输和处理过程。算术逻辑单元执行算术运算和逻辑运算。
冯·诺依曼结构的优点是灵活性和可编程性。计算机可以根据需要执行不同的指令,处理不同的数据。这种结构体系也为计算机的发展提供了方向和基础,是现代计算机体系结构的基础。

冯诺依曼体系结构
冯·诺依曼结构体系的主要思想和观点包括以下几个方面:
- 存储程序:冯·诺依曼结构体系的核心思想是将指令和数据以同等的方式存储在计算机的存储器中。这意味着计算机可以像执行数据操作一样执行指令操作,从而实现程序的存储和执行的统一。
- 结构的分离:冯·诺依曼结构体系将计算机分为五个主要部件:输入设备、输出设备、存储器、控制单元和算术逻辑单元(ALU)。这种分离结构使得各个部件可以独立地工作,并且可以根据需要进行组合和扩展。
- 指令和数据的二进制表示:冯·诺依曼结构体系要求计算机中的指令和数据都以二进制形式进行表示。这种统一的表示方式使得计算机可以通过对存储器中的二进制数据进行解释和处理来执行指令,从而实现各种运算和操作。
- 顺序执行:冯·诺依曼结构体系要求计算机按照指令的顺序进行执行。控制单元会按照存储器中指令的顺序逐步解释和执行,确保指令和数据的正确处理顺序。
- 可编程性:冯·诺依曼结构体系支持计算机的可编程性。指令和数据的存储方式使得计算机可以根据需要执行不同的指令,处理不同的数据。这种可编程性使得计算机具有广泛的应用领域,可以用于处理各种任务和问题。
冯·诺依曼结构体系的主要观点和思想可以总结为将指令和数据进行统一的存储和处理,并且通过分离的结构使得各个部件可以独立地工作。这种体系结构的优势在于灵活性和可编程性,为现代计算机的设计和发展提供了基础。同时,冯·诺依曼结构体系也为后续的计算机体系结构研究和发展提供了重要的思想和引导。通过不断的创新和改进,计算机体系结构得到了广泛的拓展和应用,为人类的科学研究和工程技术提供了强大的支持和推动力量。
你知道阿兰图灵吗?
是的,我知道阿兰·图灵。
阿兰·图灵(Alan Turing)是一位英国数学家、逻辑学家和计算机科学先驱,被公认为计算机科学之父之一。他在20世纪上半叶做出了许多重要的贡献,对计算机科学的发展和人工智能的研究产生了深远的影响。

阿兰图灵
图灵以他提出的“图灵机”而闻名,这是一种简单但功能强大的抽象计算模型。图灵机的基本原理是通过读取和写入符号的方式来操作无限长的纸带,并根据一系列预先定义的规则进行计算。这一模型为今天的计算机科学和计算理论提供了基础。
图灵还在1936年提出了“停机问题”,这是一个与计算机理论密切相关的问题。该问题询问是否有一种通用的算法能够确定给定的图灵机是否会在某个输入上停机。图灵证明了这个问题的不可解性,即无法找到一个通用的算法来解决停机问题。
在第二次世界大战期间,图灵为英国政府工作,负责解密德国的密码机“恩尼格玛”。他的工作对盟军的胜利做出了巨大贡献。由于保密原因,图灵的工作直到战后才被大众所知。
然而,图灵最为人所知的是他的思考实验,即图灵测试。这一实验提出了一个问题:当人与机器进行交互时,能否区分出机器是否具有人类智能。图灵认为,如果机器能够通过对话模拟出与人类几乎无法区分的智能回应,那么可以说机器具备了人工智能。
尽管图灵在其短暂而不幸的一生中取得了重大成就,但他的天赋和逐渐出现的性取向引起了当时社会对他的隐私入侵和歧视。他于1954年去世,享年41岁。图灵的工作和思想对计算机科学、人工智能和数学的发展产生了深远的影响,并为我们提供了一种深刻的理解和思考计算和智能的方式。
阿兰图灵的两篇著名论文是什么?
阿兰·图灵的两篇著名论文是《关于可计算数及其在判定问题上的应用》(On Computable Numbers, with an Application to the Entscheidungsproblem)和《计算机智能与智能行为》(Computing Machinery and Intelligence)。
- 《关于可计算数及其在判定问题上的应用》是图灵于1936年发表的论文。这篇论文探讨了一个被称为“停机问题”的重要计算理论问题,即找到一种算法来确定一个图灵机在给定输入上是否会停机。图灵通过引入“图灵机”这一抽象计算模型来研究可计算性的概念。他证明了停机问题的不可解性,即无法设计一个通用算法来解决所有停机问题。
- 《计算机智能与智能行为》是图灵于1950年发表的论文,也被称为“图灵测试”论文。这篇论文探讨了机器是否能够表现出智能的问题。图灵提出了一个著名的思考实验,即“图灵测试”。他认为,当一个人通过对话无法准确判断出对方是人还是机器时,这台机器可以被认为是具备智能的。图灵通过提出这一测试来探讨机器智能的概念,并对人工智能领域的发展产生了深远的影响。
这两篇论文都是图灵在计算理论和人工智能领域作出的重要贡献。《关于可计算数及其在判定问题上的应用》奠定了计算理论的基础和图灵机的概念,对计算机科学的发展产生了深远的影响。《计算机智能与智能行为》则提出了图灵测试这一重要思想,对人工智能研究和发展产生了重要影响,并成为衡量机器智能的标准之一。
,