一.一次函数的定义
一般地,形如y=kx b,(k、b是常数,k≠0)的函数,叫做一次函数,一次函数也被称为线性函数。对于其含义注意以下几点:
1.定义域:一次函数的定义域是一切实数.
2.当b=0,k≠0时,y=kx是正比例函数也是一次函数。正比例函数是一次函数的特例,一次函数包括正比例函数.
3.当k=0,b≠0,它不是一次函数,属于常值函数。一般地,我们把函数y=b(b为常数)叫做常值函数.它的自变量由所讨论的具体问题确定。
二.函数的图像与性质

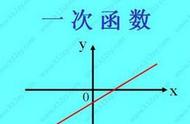
注意‼️一次函数y=kx b,(k、b是常数,k≠0)的图像是一条直线。
当b>0时,直线y=kx b是由直线y=kx向上平移|b|个单位长度得到;
当b<0时,直线y=kx b是由直线y=kx向下平移|b|个单位长度得到。
三:k、b对一次函数y=kx b的图象和性质的影响:
1.截距:直线y=kx b的截距是b,即:一条直线与y轴的交点的纵坐标叫做这条直线在y轴上的截距,截距可以为负也可以为正。
2.增减性:k>0,y随x的增大而增大;k<0,y随x的增大而减小。
3.倾斜度:|k|越大,图象越接近于y轴;|k|越小,图象越接近于x轴。这个常数k称为直线的斜率.
总之,k决定直线y=kx b从左向右的趋势,b决定它与y轴交点的位置,k、b一起决定直线经过的象限。
四.两条直线:y=kx1 b1和:y=kx2 b2的位置关系

五.正比例函数与一次函数及性质