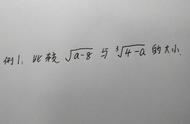二分法,顾名思义,即是在某个区间内进行二分查找,取中间值的意思,我们以为例:
已知;
则取与的中间点,因为,则再取与的中间值,以此类推下去。
因为非完全平方数算术平方根是无理数,所以算得的区间会无限接近于这个无理数,由此可见,每计算次,所得的结果的误差也就不超过
类似地,还有一种方法叫做逐次逼近法,我们以为例,我们知道,为了计算的小数点后一位,我们可以把、、……全部算出来,当算到,时,我们就可以确定小数点后一位数字,以此类推,我们把,……计算出来,与比较,从而得出小数点后两位……这样,每进行次运算(最坏情况),误差就不大于
但是,用这种方法,越到后面,计算量就越大,但是进步不快,有没有更加简便的方法呢?
平方法这种方法,主要是以不等式的计算规律,来加快计算速度,我们还是以为例,我们知道
把上式两端各减去,得
上式平方,得
上式平方,得
上式平方,得
上式左右同除以,得
整理,得
观察上式,我们可以看出,我们求出的区间的误差不超过,这比上一种方法计算量要小得多,而且每次取得的进步是平方级别的,按照这样,我们可以算出的小数点后许多位,例如上式,我们化成小数后,得出的范围是。
我们不妨求解地更精确一些,例如从一开始,我们就可以把缩小到更小的范围:
平方,得
再平方,得
再平方,得
再平方,得
同除以,得
整理后化成小数,得
这样,我们就把算到了小数点后第位,仅仅通过次计算,我们就可以使算得的结果与相差不超过!
由此,我们可以证明一下用这种方法,误差是否会越来越小。如果是的近似值,且已知误差()。我们可以取一个更好的近似值(当时),使得
和的误差满足:
我们将不等式两端平方,得
两边同除以,得
当时,,可见的误差比更小。
此外,把不等式两边同时立方,甚至次方,次方,都会得到更加精确的近似值,但是平方较为简单,而多次平方会使误差更小。此外,还可以用这种方法去求一个数立方根的值。
线性穿插法这种方法利用了算术平方根与完全平方数的性质,我们还是以为例。
把放在中间设为,分别找到前后完全平方数:,
线性穿插,得:
我们再以为例,,
线性穿插,得:
类似地,我们设所求的平方根为,两个完全平方数的算数平方根分别为,,我们得到:
因式分解,得,
整理,得
由此,我们可以推导出
因为,所以只取正根,即
这便是线性穿插法的通解。
极限法极限法的原理为当趋近无穷小时,有,其中为不为的常数。
我们以为例,因为
变形,得
我们设所求的算术平方根里面的数为,比它略小的完全平方数为,则
通过上面的变换,我们得到:
这便是极限法的通解。
附录- 实现二分法
double kaifang(double low,double up){
double x=up;
double mid=low (up-low)/2;
while(fabs(mid*mid-x)>=1e-6){
mid=low (up-low)/2;
if(mid*mid>x){
up=mid;
}
else if(mid*mid<x){
low=mid;
}
}
return mid;
}
本文作者:
完成时间:
,