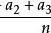一、选择题
1.若分式2
x 3
有意义,则x 的取值范围为( )
A. x 3 B. x 3 C. x 0 D. x 3
2.下列各式的变形中,正确的是( )
A. 1 1 x
x
x x
B.
2 2 x 4x 3 x 2 1
C. 2 1
x x x 1
x
D.
2 2 ( x-y)( x y) x y
3.把x2 x m因式分解得( x-1 )( x 2),则m的值为( )
A.2 B.3 C. 2 D. 3
4.科学家发现了一种新型病毒,其直径约为0.00000012mm,数据0.00000012用科学记数法表示正确
的是( )
A. 7 1.2 10 B. 7 1.2 10 C. 8 1.2 10 D. 8 1.2 10
5.已知a2 b2=12,ab=﹣ 3,则(a b) 2 的值为( )
A.3 B.6 C.12 D.18
6.等腰直角三角形的底边长为5cm,则它的面积是( )
A.25cm2 B.12.5cm2 C.10cm2 D.6.25cm 2
7.下列说法中,正确的是( )
A.两腰对应相等的两个等腰三角形全等
B.两锐角对应相等的两个直角三角形全等
C.两角及其夹边对应相等的两个三角形全等
D.面积相等的两个三角形全等
8.如图,在△ ABC中, AB=4,AC=6,∠ ABC和∠ ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC
于M、N,则△ AMN的周长为( )
A.10 B.6 C.4 D. 不确定
9.如图,在△ ABE中, AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠ BAE的度数是
( )
A.80°
B.85°
C.90°
D.105°
10.如图,在四边形ABCD中,∠ A=60°,∠ B=∠D=90°, AD=8, AB=7,则BC CD等于( )
A.6 3 B.5 3 C.4 3 D.3 3
11.如图,在△ ABC中,点D在BC上, AB=AD=DC,∠ B=72°,那么∠ DAC的大小是( )
A.30° B.36° C.18° D.40°
12.一个多边形的每个内角都等于144°,那么这个多边形的内角和为( )
A.1980° B.1800° C.1620° D.1440°
13.如图,∠ AOB 是平角,∠ AOC=50°,∠ BOD =60°, OM 平分∠ BOD,ON 平分∠ AOC,则∠ MON 的度数
是( )
A.135° B.155° C.125° D.145°
14.如图,∠ A ∠B ∠C ∠ D ∠E ∠F 的度数是( )
A.360° B.480° C.540° D.720°
15.下列计算中,正确的是( )
A.a 3 a2=a5 B.(2a) 3=6a3 C.a 5÷a2=a3 D.(a 1) 2=a2 1
二、填空题
16.已知关于x 的方程2
3
2
x m
x
的解是正数,则m的取值范围是__________ .
17.若 y2 my 16是完全平方式,则 m ___.
【答案】8
18.如图, BD平分∠ ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC= 8. 若S△ABC=21,则DE=________ .
19.用7 根火柴棒首尾顺次连接摆成一个三角形,能摆成不同的三角形的个数为_____.
20.在△ ABC中,已知∠ ABC=44°, D为边BC上的一点,满足DC=2AB,∠BAD=24°,则∠ ACB的大小为
_____.
三、解答题
21.列方程解应用题:
商厦进货员预测一种应季衬衫能畅销市场,就用8 万元购进这种衬衫,面市后果然供不应求;商厦又用
17.6 万元购进了第二批这种衬衫,所购衬衫数量是第一批购进量的2 倍,但单价贵了4 元.
(1)第一批和第二批共购进衬衫多少件?
(2)商厦销售这种衬衫时,每件定价都是58 元,如果把所有衬衫都售完,商厦共盈利多少元?
22.分解因式
(1) 16a2 1; (2) 2 x 14x 49
23.请把下面的推理过程补充完整,并在括号内注明理由. 如图, ABE CBD , BA BE ,
A E , ED 交BC 于点F ,且FBD D. 求证: AC BD .
证明:∵ ABE CBD (已知)
∴ ABE EBC CBD EBC (______)
即ABC EBD
在△ABC和△EBD 中,
ABC EBD
A E
∴△ABC≌△EBD (______)
∴ C D ( ______)
∵ FBD D
∴ C ______(等量代换)
∴ AC BD (______)
24.如图,已知直线l 和l 外一点P,用尺规作l 的垂线,使它经过点P.(保留作图痕迹,不写作法)
25.一个正多边形中,一个内角的度数是它相邻的一个外角的度数的3 倍.
(1) 求这个多边形的每一个外角的度数;
(2) 求这个多边形的边数.
【参考答案】***
一、选择题
题
号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答
案
A D C B B D C A C B B D C A C
二、填空题
16.m>-6 且m-4
17.无
18.3
19.2
20.22°
三、解答题
21.( 1)6000(2)两次生意共获利润92000 元
22. 1 4a 1 4a 1 ;
2 2 x 7
23.等式性质, AB BE,ASA,对应角相等,∠ FBD,内错角相等,两直线平行
【解析】
【分析】
根据全等三角形的判定与性质即可求解.
【详解】
证明:∵ ABE CBD (已知)
∴ ABE EBC CBD EBC (等式性质)
即ABC EBD
在△ABC和△EBD 中,
ABC EBD
AB BE
A E
∴△ABC≌△EBD (ASA)
∴ C D (对应角相等)
∵ FBD D
∴ C ∠FBD(等量代换)
∴ AC BD (内错角相等,两直线平行)
【点睛】
此题主要考查全等三角形的判定,解题的关键是熟知ASA进行判定三角形全等.
24.详见解析
【解析】
【分析】
以P 为圆心,以任意长为半径画弧,交直线l 与于点M、N,再分别以点M、N为圆心,以大于
1
2
MN长为
半径画弧,两弧相交于点G、H,连接GH,直线GH即为所求.
【详解】
如图,直线GH即为所求.
【点睛】
本题考查的是作图- 基本作图,熟知线段垂直平分线的作法是解答本题的关键.
25.(1)45 °; (2)8.