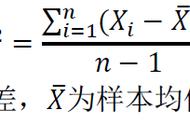标准偏差计算中的样本量补偿
本文讨论了贝塞尔校正,这有助于我们更准确地估计某些参数和长时信号的标准偏差。
本文是我们针对电气工程师的统计数据系列的延续,其中第一个介绍了统计数据,作为分析电路行为和表征工程系统的方法。然后,我们讨论了特定的方法-尤其是使用平均值和中位数来找到数据集的集中趋势。最近,我们介绍了三种统计性描述量度-平均偏差,标准偏差和信号处理中的方差,以了解与这些中心趋势的偏离。以我们上一篇有关标准差的文章为背景,我们现在可以讨论该讨论的另一个关键方面:标准差计算中的样本量补偿。
除以N还是N–1?
如果您已阅读上一篇文章,也许您会注意到在计算离散数据的标准偏差时所使用的公式中的明显差异。公式如下:

标准偏差表示信号随机偏差的平均功率。但是,当我们计算某物的平均值(即算术平均值)时,我们总是除以N(其中N表示数据点的数量),而不是除以N-1。
为什么在计算标准偏差时使用N-1?
实际上,我们并不总是除以N-1。我们可以使用N而不是N–1来计算标准差,但是从理论上讲,所得的数字表示不同的东西。我强调“理论上”,因为在电气工程的情况下,差异通常很小。尽管如此,重要的是要了解基本概念,该概念植根于样本与总体之间的差异。
样本,总体和标准偏差
假设购买了一个运算放大器(零件编号为OPA100),并在实验室进行了一些实验后,您意识到数据表中的规格不能为您提供有关应用工作温度下输入失调电压的足够信息。为了解决这个问题,您决定购买15个OPA100运算放大器(因此N = 15),进行一些测量,并根据该样本生成一些统计数据。
如果OPA100在相关工作温度下的典型失调电压为1 mV,则15个分量样本中的失调电压分布可能如下所示:

随着样本数量的增加,测得的分布将更接近正态分布。
您已经测量了每个组件的偏移电压,现在可以计算标准偏差,但是首先,您需要问自己一个问题:我要计算样本还是总体的标准偏差?换句话说,我应该在我面前报告这15个组件的标准偏差,还是应该尝试报告适用于所有OPA100运算放大器的标准偏差?
样品的标准偏差
如果我们正在处理一个样本,并且想知道该样本的标准偏差,则除以N。这是有道理的-如上所述,在计算算术平均值时,我们总是除以N,并且标准偏差涉及数据集中偏差乘方的算术平均值。
因此,继续我们的示例,除以N会告诉您所购买的15个OPA100运算放大器的标准偏差。

垂直线表示电压值,该电压值是样本平均值上下的一个标准偏差。在计算标准偏差时,我用N除以。
电气工程师经常遇到的另一种数据集是数字化电压信号,正如我们在前一篇文章中所看到的,标准偏差是一种量化电气噪声的方法。
如果您想知道所采集信号的标准偏差,即被数字化并存储在内存中的特定电压电平,则在计算标准偏差时将除以N。在这种情况下,所获取的信号是统计样本。
总体标准差
如果我们正在处理样本,并且想知道总体的标准差,则可以除以N–1。“总体”是指所获得的数据点为其提供代表性样本的整个群体。使用N-1而不是N是一种补偿与有限样本量相关的误差的方法。该技术称为贝塞尔校正。
需要进行校正是因为如果要计算总体的标准偏差,则应使用总体平均值。但是我们通常无法获得总体均值。我们只有样本均值,它是总体均值的近似值。事实证明,当我们使用样本平均值而不是总体平均值时,标准偏差始终较低,并且用N-1(而不是N)除以减轻这种影响。
因此,如果要估算所有已制造的OPA100运算放大器的偏置电压的标准偏差,则应从15个分量的样本中收集数据,然后在计算标准偏差时将其除以14而不是15。
垂

直线表示电压值,该电压值是样本平均值上下的一个标准偏差。在计算标准偏差时,我用除以N-1。
同样,如果要基于相对较短的数据采集时间来量化电压信号的噪声,则可以除以N-1。在这种情况下,数字化数据就是样本,信号本身就是群体。
您还可以这样认为:当我们除以N-1时,我们将重点放在在分析信号中产生噪声的潜在过程上,而不是在由采集信号所代表的时间段内测量这些过程的影响。
样本量的影响
工程师的直觉可能会告诉您,贝塞尔的校正不是那种会影响或破坏您的分析的事情,在许多情况下,这是正确的。在工程应用中,我们经常有大量的数据,并且我们直观地认识到这些大数据集将产生一个样本均值,就所有实际目的而言,该均值与总体均值相同。因此,无需除以N-1即可除以N。
但是,我们应该记住,这种关系已内置在更正中。随着N的增加,相对于整体计算,N和N-1之间的差异变得不那么重要。因此,当需要进行补偿时(即,样本量较小时),使用N-1可施加理想的补偿;而当不需要补偿时(即,样本量较大时),则N-1不会产生明显的影响。
结论
我们已经看到,可以根据分析意图和样本量以不同方式计算标准偏差。在下一篇文章中,我们将探讨标准差与均方根值之间的关系。
,