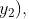人类采取的行动及静态奖励模型
五、奖励催生状态簇
第二个实验的目标是确定奖励是否会催生状态簇。我们预测,即使图结构本身不会催生状态簇,但奖励相同的临近节点也会聚集在一起。
Solway等人的研究发现:人类更喜欢跨越最少分层边界的路径[2]。因此,在两条完全相同的路径中做选择时,选中其中一条路径的唯一原因是它跨越了较少分层边界。对此,有些人可能会反驳,认为人们其实更倾向于选择奖励值更高的路径。然而,在接下来详述的设置方法中,智能体只有在实现目标时才能获得奖励,而不是在路径的“行走”过程中积累奖励。此外,奖励值的大小在不同的实验中也有所不同。因此,人们不太可能因为节点的奖励值更高而选择某条路径。
5.1 设置
该实验是在网页上进行的,使用了亚马逊土耳其机器人(MTurk)。实验参与者要执行下述任务:
想象你是一名矿工,在由隧道连接的网状金矿中工作。每个矿每天会产出一定数量的黄金(用数值表示)。你的日常工作是从起始矿井导航到目标矿井,并从目标矿井内收集黄金。在某些时间段内,你可以根据喜好自由选择矿井。这时你应该尝试选择黄金数值最高的矿。在另外一些时间段,你只能开采一个金矿,该矿井的黄金数值会被标记为绿色,其他矿井标记为灰色。这时你应该导航到可开采的矿井。每个矿井的黄金数值都会在矿井上作标记,当前矿井将用粗边突出显示。你可以使用箭头键(上、下、左、右)在矿井间导航。到达目标矿井后,你可以按空键来收集黄金数值,周而复始。这个实验将持续100天。
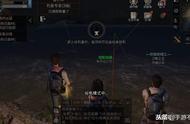
将下图(左侧部分)展现给参与者。与之前的实验一样,为了控制潜在的左右非对称性,我们给参与者随机分配同一图中的布局构造或水平翻转版本,还描述了预期催生出的状态簇,节点编号供参考(右侧部分)。

向MTurk参与者展示的矿井分布图(左)和可能存在的状态簇(右)
我们将第一种情况称为“自由选择”(free-choice),参与者可以自由导航到任何矿井,将第二种情况称为“固定选择”(fixed-choice),参与者需导航至指定矿井。为阻止随机反应,参与者在每次试验中都会得到金钱奖励。
在每次试验中,奖励值的变化概率为0.2,新的奖励值从区间[0,300]中随机抽取。然而,奖励的分组在试验中保持不变:节点1、2和3的奖励值始终只有一个,节点4、5和6的奖励值不同,节点7、8、9和10有第三个奖励值。
前99个试验使参与者能够建立状态簇的层次结构,最后一次试验(以测试试验的形式进行)要求参与者从节点6导航到节点1。假设奖励催生出上面所示的状态簇,我们预测,选择通过节点5的路径的参与者会比选择通过节点7的路径的参与者更多,因为节点5只跨越一个簇边界,而节点7跨越两个簇边界。
5.2 推论
我们对固定选择案例进行建模,假设100个试验中的全部任务与提交给参与者的第100个试验(即测试试验)相同。首先,我们提出静态奖励假设,即在所有试验中奖励保持不变。接着,我们又提出动态奖励假设,即每次试验中奖励都会发生变化。
与之前的实验不同,参与者选择一个模型预测的节点,而本实验关注的是,参与者选择的完整路径中,第二个从起始节点到目标节点的节点。因此,为了将模型与人类数据进行比较,我们使用宽度优先搜索算法(breath-first search)的改进形式(以下称为“分层BFS”)来预测从起始节点(节点6)到目标节点(节点1)的路径。
静态奖励
对于每个主体,我们使用Metropolis-within-Gibbs算法从后验样本中进行采样,并选择最可能实现的分层结构,比如后验概率最高的分层结构。然后,我们使用分层的BFS首先在状态簇之间寻找路径,然后在状态簇内的节点之间寻找路径。
动态奖励
我们使用在线推断方法进行动态奖励。对于每个仿真参与者,我们只允许每个试验的取样进行10步。然后,我们保存了分层结构,并添加了经过修改的奖励的信息。接下来,我们从保存的分层结构开始,再次进行采样。在人类实验中,每次试验开始时,尽管状态簇内的奖励值总是相等,但为奖励重新赋值的概率始终为0.2。这种推理方法模拟了人类参与者在许多试验过程中如何累积学习。为了达到此实验目的,我们假设人们一次只能记住一个分层结构,而不是同时更新多个分层结构。我们还修改了对数后验(log posterior),以惩罚非关联的状态簇,因为利用在线推断方法时,非关联的状态簇更加常见。
5.3 结果
人类组和两个仿真组均有95名参与者。空假设(null hypothesis)由数量相等的参与者选择通过节点5和通过节点7的路径来表示,因为在没有任何其他信息的情况下,假设两条路径的长度相等,参与者选择任意一条路径的概率均为50%。

人类采取的行动、静态奖励模型和动态奖励模型
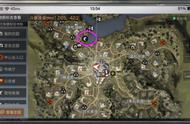
如上表所示,人类实验和静态奖励建模的结果在 α=0.05 时具有重要的统计意义。此外,如下图所示,人体实验的预期结果在以0.5为中心的正态分布的第90百分位处,这也是空假设的预期比例。图中包括由静态奖励模型(第一行)确定的状态簇、可在非关联成分的惩罚项间形成状态簇的静态奖励模型(第二行)以及动态奖励模型(第三行)。

仿真识别的的状态簇
静态奖励
我们使用了Metropolis-within-Gibbs算法的1000迭代生成每个样本,每个样本的可靠性参数和采样间隔均为1。静态奖励下的仿真结果是参与者倾向于通过节点5的路径,达到统计上的显著性水平。此外,由于其目的是对人类行为进行建模,鉴于人类数据在统计学上也具有显著性(0.0321lt;α=0.05),该结果有意义。