帅气的香农(图片来源:Konrad Jacobs,Erlangen)
1948年,当香农终于整理好所有文字,发布他那惊天论文——A Mathematical Theory of Communication(一种通讯的数学理论)——的时候,不知道他是否会知道,自己会在一年后,会和瓦伦·韦弗(Warren Weaver)一道,将A改成The,完成用一篇论文建立一个学科的壮举。
我们身处信息时代,但在享受海量数据带来的便利时,克劳德·香农(Claude Shannon,1916-2001)——信息论的创始人,却鲜为人知。香农是近代最伟大的数学家之一,他毫无疑问是个天才,并且拥有符合所有人刻板印象的,只有天才才能拥有的离谱人生。毕竟只用一篇论文就能建立一个学科的,除了爱因斯坦,还有香农。
小说中才会有的天才
香农1916年出生于密歇根州的一个小镇,自幼崇拜托马斯·爱迪生,经常在家里制作模型飞机、遥控船还有无线电台。后来他才知道,原来爱迪生竟然是自己的远房亲戚。
1932年香农进入密歇根大学,就是在那里,他接触到了乔治·布尔(George Boole,英国数学家,布尔型、布尔代数均得名于他)的理论。大学毕业时,他获得了电子工程和数学两个学士学位,并进入麻省理工学院深造。在那里,他参与了万尼瓦尔·布什(Vannevar Bush)的微分分析机的相关工作。微分分析机是一种由轴承和齿轮构成的机械计算机,正是在那时,他发现布尔代数与这种机械、电路设计,有惊人的联系。于是他发表了自己的硕士论文,《继电器和开关电路的符号分析》(A Symbolic Analysis of Relay and Switching Circuits)。从此,电路设计从依靠灵光一闪的艺术,变成了可以依靠严谨逻辑一步步推导下来的工程。
“这可能是本世纪最重要、最著名的硕士学位论文。”哈佛大学的霍华德·加德纳(Howard Gardner)在后来这样评论这篇论文。不过,即使是这样的成就还远不能称为香农最高光的时刻。
香农在万尼瓦尔·布什的建议下,将他的理论应用于遗传学。当时沃森和克里克还没有弄清楚DNA的结构,但是既然遗传物质必然包含信息,概率一类的东西,为什么不尝试一下呢?在读了所有他能找到的有关遗传学的书后,香农撰写了《理论遗传学的代数》(An Algebra for Theoretical Genetics),用线性代数描述不同遗传性状在遗传中的可能性。以此,就能用线性代数来预测性状是如何代代相传的。不过,这种理论并没有被生物学家大规模使用。但至少,1940年香农以此得到了麻省理工学院的博士学位,和在普林斯顿高等研究院的工作。而在那里,他可以接触到那个时代最闪耀的一批人——阿尔伯特·爱因斯坦、库尔特·哥德尔、冯·诺依曼……

物理学圣地,普林斯顿高等研究院(图片来源:Hanno Rein,Wikipedia)
在这批人的光芒的掩盖之下,即使是当时的香农,也不过是一个初出茅庐的毛头小子。按照香农的说法:“我见过这些人,可是他们没有见过我。”那时信息论已经在他头脑中酝酿。但他失望地发现,在普林斯顿高等研究院中,所有人关心的都是一些量子力学、广义相对论的本质之类的问题,他那些更实用一些的数学问题并没有人关心。
无人关心,再加上二战的爆发,他只在高等研究院待了两个月,就加入了贝尔实验室,在军方的直接领导下研究火控系统和密码学。根据《香农传》(The Bit Player)中,对香农前妻、前女友和妻子三人的采访,可以知道香农是一个帅气且有情调的人。而正是在军方领导的贝尔实验室工作时,他甚至无法维持和第一任妻子的婚姻,可见这段经历让他有多消沉。
不过在贝尔实验室的工作也不是全是坏事,至少他接触到了艾伦·图灵(Alan Turing),并得知了他的“图灵机”。他对此很感兴趣,并经常约在下午茶时间见面,香农还为图灵机补充了一些自己的见解。
按照香农的说法,在贝尔实验室密码学方向的工作,只是为自己提供一个职位,让自己能研究自己真正关心的,有关信息的数学。其实,1945年二战末期,他在贝尔实验室内部密码学相关的备忘录中,就已经有了信息论的雏形。至于为何要等到1948年才整理出完整的论文,他的回答只有一个字:“懒。”
一篇论文建立一个学科
1905年,26岁的爱因斯坦发了四篇论文,建立了三个学科——量子论、统计力学和狭义相对论。43年后的1948年,当年面对爱因斯坦插不上话的香农,在32岁时终于也完成了一篇论文建立一个学科的壮举——A Mathematical Theory of Communication(一种通讯的数学理论)横空出世,其完整性甚至到今天还能作信息论教材使用。一年后,用这篇论文再加上瓦伦·韦弗(Warren Weaver)的科普文章,把A改成The,两人出版了The Mathematical Theory of Communication(通讯的数学理论)。信息论就此诞生。
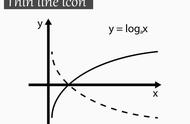
信息的数量与其内容好坏无关,毕竟所有信息编码转换成信号后,发送时的数量只与其长度有关,而这个长度可以用对数很方便的表示。受约翰·图基(John Tukey,快速傅里叶变化发明者)的启发,香农用信息转换成二进制数字后的二进制数位(binary digit)作为信息的单位,或者将其简称为比特(bit)。这是比特这一词首次公开出现,这个词在接下来大半个世纪的时间里,深刻地改变了整个世界。(以下出现的对数log均以2为底)
但仅仅找到信息的单位还远远不能让香农满足,他想要更深刻的解释。
用一种不太严谨的说法,在他看来,能从随机过程结果的不确定性结果中,让人确定唯一结果的东西才是信息。
比如说,抛出一枚硬币,落地时数字面和花面朝上概率相等。那么在不知道结果前,都不能十足的把握说硬币哪面朝上。但如果知道了硬币数字面朝上的信息,那么就可以确定抛硬币的结果是数字面朝上。如果抛出一枚两边都是数字面的硬币,那么就算不知道结果的信息,也可以确定硬币的数字面朝上。两种抛硬币的问题,前者在确定答案需要信息,而后者不需要。
再加上一些数学概率上的考虑,香农发现玻尔兹曼曾经研究过的物理学概念——熵,很适合用来描述这些。

其中pi是可能发生某种结果的概率,H就是信息学中的熵,或称香农熵(Shannon entropy),单位为比特。它和玻尔兹曼总结的热力学中物理上的熵只差了一个常系数kB·ln2,kB是玻尔兹曼常数,ln2而是因为信息论和物理学中对对数底数选择的不同导致的。
信息熵就是信息数量的度量,我们由此可以计算一个符号中包含的信息量了。
对于抛一枚硬币的问题,两面概率都是1/2,则其信息熵为H=-(0.5×log(0.5) 0.5×log(0.5))bit=1 bit。对于两面相同的硬币,则是H=-1×log(1) bit=0 bit。如果不考虑大小写区别,那么如果26个英文字母再加上空格,27个符号,发送信息时,如果每个符号出现的概率相等,并且相互独立,那么每个符号包含的信息将会是H=-log(1/27)bit≈4.75bit。
在这种情况下,再加上大写、标点、其他语言的符号,零零散散的其他符号凑到一起,可以将8比特定义为1个字节(Byte),不过那已经是后话了。
实际情况中,这27个符号出现的概率并不相等,并且符号之间也存在关系,即使不考虑大范围(8个英语符号以上)上字母、单词之间的联系,单个英文符号中的信息熵其实也不过是4.75bit的一半。剩下的50%,就是英文的冗余度。换句话说,在大多数情况下,即使英文中去掉了50%的字母,其实并不影响英语的理解。就像在速记时,经常省略元音字母,却不影响对英语的理解。
解释完信息,香农可以开始认真讲述他关于信息的传递,也就是通信的看法。