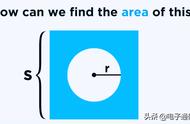
围成平面区域的曲线可用三种不同的形式表示:
1、直角坐标系:
己知在区间〔a,b〕上的非负连续曲线 y = f(x)、x轴及二直线x = a 与 x = b 所围成的曲边梯形的面积
就是〔a,b〕上 f(x)的定积分。
注:面积不能是负数,所以要求函数是非负的,若函数f(x)有负的部分,
则积分部分为 ∫丨f(x)丨dx 。(在闭区间【a,b】上)
例题1、y=x^2与x=y^2围成图形的面积该怎么求?

例题1图(1)
解:两条曲线的交点是(0,0)与(1,1),则此区域的面积为:
A=亅(√x - x^2)dx = 1/3 。 (在闭区间【0,1】上积分)
注:闭区是〔0,1〕,是对x积分把x=y^2用x来表示y,即 y = √x 。
2、参数方程:
例题2、求椭圆: x = acost ,y = bsint (0≤ t ≤ 2Π)的面积。
解:椭圆关于 x 轴、y 轴都对称,其面积是第一象限那部分区域面积的四倍。
第一象限那部分区域是曲线
x = acost ,y = bsint ,(0≤ t ≤ Π/2) 和 x 轴、y 轴所围成。
而函数 x = acost 在【0,Π/2】严格减少,则有 x' = -asint ≤ 0 。
由积分面积公式 A = ∫∣y∣dx (在闭区间【a,b】上积分)得:
椭圆的面积 A = -4∫∣ bsint∣(-asint)dt = 4ab∫sin^2tdt
= 2ab∫(1 - cos2t)dt = 2ab(t-1/2 sin2t) ∣
= abΠ
注:积分区间为【0,Π/2】。
3、极坐标(略):
注:做此类题要明白是对谁求积分、找出闭区间、会用不定积分常用公式。