1、从个位向左和向右每2位数分一节,左边是整数右边悬小数,最左和最右一节可能是2位也可能是1位数。整数部分和小数部分各分出几节说明平方根就有几位整数和小数。
2、求出最高(左边第一节)节位平方根(整数),余数连接下一节2位数作为下一组的被除数。|
3、用求出的平方根×20
后试除被除数,能商几就用被除数 --(平方根×20 商)x商。这个商就是所求平方根的第2位数。
4、同上:将第二次的余数连接下一节2位数作为新的被除数。
5、将前面已有两位数组成的平方根×20后试除新的被除数,能商几就用:(前两位平方根×20 商)×商。这个商就是所求平方根的第3位数。
6、反复采用上述计算方法,直到余数是0为止。通过试商,如果发商大或商小了就减小或增大数字就行了。总之求出的平方根必须与题目相符。
例:1
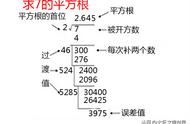
求465124的平方根
解:
分节为:46 ’ 51 ’ 24
46的平方根(整数部分)是6
6×6=36
46-36=10
1000 51=1051
6×20=120
1051÷120最多能商8
1051 -(6×20 8)×8
=1051-1024=27
2700 24=2724
68×20=1360
2724÷1360最多可以商2
(68×20+2)×2
=2724
2724--2724=0
600 80 2=682
465124的平方根是682
例:2
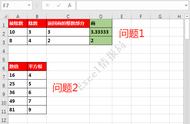
求15625的平方根
解:
分节为:1 ’ 56 ’ 25
1的平方根是1
1×1=1
1×20=20
56÷20最多能商2
56 --(1×20 2)×2
=56--44=12
1200 25 1225
12×20=240
1225÷240最多可以商5
(12×20+5)×5
=1225
1225--1225=0
100 20 5=125
15625的平方根是125
,