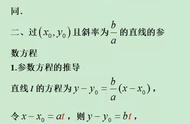高考数学选做题,参数方程的考查重点在于对参数t的几何意义的理解和应用。在近几年的考题中着重考查参数t在标准和非标准参数方程中几何意义的区别。下面将其规律和应用程序归纳如下:
一、参数t的几何意义
1.过定点M0(x0,y0),倾斜角为α的直线的参数方程为x=x0 tcosα,y=y0 tsinα(t为参数)①
通常称①为直线l的参数方程的“标准式”.其中参数t的几何意义是:|t|是直线上任一点M(x,y)到M0(x0,y0)的距离,即|M0M|=|t|.
若直线上任意两点P1,P2对应的参数分别为t1,t2,则|P1P2|=|t1-t2|,P1P2的中点对应的参数为1/2(t1 t2).
对于参数方程形如x=x0 tcosα,y=y0 tsinα(t为参数)的直线,当a2 b2≠1时,应先化为标准形式后才能利用t的几何意义解题.
2.参数t经常用在直线截圆锥曲线的弦长和距离问题中,解题时通常过某定点作一直线与圆锥曲线相交于A,B两点,所求问题与定点到A,B两点的距离有关.解题时主要应用定点在直线AB上,参数t的几何意义,结合根与系数的关系进行处理,巧妙求出问题的解.
二、参数方程解题程序
将普通方程化为参数方程时.一般只涉及直线、圆、椭圆及抛物线的方程变化,所以一定要熟记它们的参数方程,并且会运用参数方程解决相关问题.破解此类题的关键点如下.
①根据曲线的类型确定参数及参数方程的曲线形式.
②根据题意直接写出特殊曲线的参数方程;当涉及动点问题时,设所求点的坐标为(x,y),利用已知点与所求点坐标间的关系及相关点法求参数方程.
③根据题目中的几何条件,确定参数的范围.

经典例题:[2008全国卷,22,10分]
在直角坐标系xOy中,曲线C1的方程为y=k|x| 2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2 2ρcosθ-3=0.
(1)C2的直角坐标方程;
⑵若C1与C2有且仅有三个公共点,求C1的方程.
思路分析:(1)运用公式代入化简即可求值;(2)由题知曲线C1是过定点(0,2)且关于y轴对称的两条射线,结合圆心到直线的距离等于半径时,一条射线与圆相切可求得k值.

总结:求解本题时应借助数形结合思想判断曲线C1的方程为y=k|x| 2与圆C2有三个交点的条件.