局势风云变幻,一时茫然不知所措。也许静下心来做两道题才是真正的幸福所在。
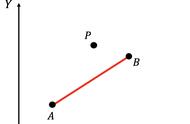
平面向量是研究几何的工具,亦是解题的神器。中学关于平面向量的内容不多,主要是概念与简单运算、坐标与简单应用。但要求却并不低,往往以选填题的压轴出现。这样的试题多半具有强烈的几何意义,旨在考查数形结合的思想。



选项A与B皆是考查向量的投影,所谓投影即是向量的模乘以夹角的余弦值。投影给出了向量数量积的几何意义。显然,投影只与向量的模和夹角有关。
由于余弦值可正、可负、可为零,所以投影亦是如此。注意投影与射影的差别,后者非负。新教材修订了投影的概念,引入了投影向量,也即是在投影的基础上乘以一个单位向量。
选项C和D的运算量较大,为了便于化简,法2采用圆的参数方程。注意参数方程中的角参是旋转角,范围取0°到360°,但不共线,所以要剔除0°和180°。通过垂直建立关于参数λ的一元二次方程,其判别式恒正,即方程有两根,也即存在两个向量。
选项D在C的基础之上,消去角参,建立关于λ的函数,求得最大值。这里如果选择消去参数λ,则会陷入计算陷阱而无法自拔。

法1与法2从代数的角度剖析,法3则从几何的角度拆解。向量是几何的工具,是解题的方法,也是一种思想。向量本身蕴含着几何意义,因此利用几何分析是理所应当。
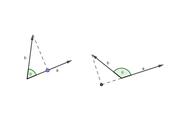
本题中的垂直隐含着圆,即点C在以AB为直径的圆上。不难发现,该圆与菱形的对角线有两个焦点,也即是有两个向量满足。
更进一步,点C的轨迹是一个椭圆,且与大圆内切于点D。当OP与x轴重合时,模长最大,也即是大圆的半径。但此时两个向量共线,不满足题意。
还是那句话,基础不牢,选完A就跑。你是否发现,多选比单选更容易得分?