1.两个向量的数量积定义
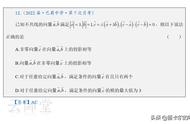
两个向量的数量积的定义为a∙b=|a||b|cosθ,其中θ为两个向量之间的夹角,两个向量数量积的结果是一个标量(只有大小、没有方向)。其含义为向量a的长度|a|与向量b在a方向的投影|b|cosθ的乘积。

角θ的取值范围为闭区间[0,π],当θ=0时,a、b共线且方向相同,其数量积为两者的模的乘积;当θ=π时,a、b共线且方向相反,其数量积为两者的模的乘积再乘-1;当θ=π/2时,a、b互相垂直,数量积的结果为0;当0<θ<π/2时,cosθ为正,数量积的结果为正数;当π/2<θ<π时,cosθ为负,数量积的结果为负数。
2.向量数量积的运算性质两个相同向量的数量积为

根据定义,向量数量积的交换律成立,即

向量之和的投影等于向量投影之和,则结合律也成立