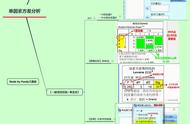
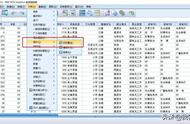
KMO检验和Bartlett球形检验。如图22-11所示,KMO检验研究变量间的偏相关性,计算偏相关时控制了其他因素的影响,所以比简单相关系数要小,一般KMO统计量大于0.9时效果最佳,0.7以上可以接受,0.5以下不宜作因子分析,本例KMO取值0.857进一步印证了作因子分析的必要性。
Bartlett球形检验统计量的Sig值小于0.01,由此否定相关矩阵为单位阵的零假设,即认为各变量之间存在显著的相关性,这与从相关矩阵得出的结论致。

公因子提取的方差。给出了公因子对初始变量方差的提取情况,也就是常说的变量共同度。其中的“提取”栏就是变量共同度的取值,代表了所有公因子能够解释的每个变量方差的比例,本例的方差提取多数都在70%左右,可见公因子对变量方差的解释效果可以接受。

方差解释表。方差解释表给出了每个因子所解释的总方差比例,以及所解释方差的累计和。观察初始特征值的“累积%”一列,前8各公因子的特征值都大于1,且解释的累计方差达到了68.558%,也就是说总体近70%的信息可以由这8个公共因子来解释,本例就取这前8个公因子进行分析。
最后一栏“旋转平方和载入”表示经过因子旋转后得到的新公因子的方差贡献值、方差贡献率和累计方差贡献率,可以看到和未经旋转相比,每个因子的方差贡献值有变化,但累计方差贡献率不变。

方差解释表,是关于初始特征值(也就是方差贡献)的碎石图,从图中看第1个公因子的方差解释贡献最大,随后因子的方差贡献趋缓。